Observation of bright polariton solitons in a semiconductor microcavity

Abstract

Microcavity polaritons are composite half-light half-matter quasiparticles, which have recently been demonstrated to exhibit rich physical properties, such as non-equilibrium condensation, parametric scattering and superfluidity. At the same time, polaritons have important advantages over photons for information processing, because their excitonic component leads to weaker diffraction and stronger interparticle interactions, implying, respectively, tighter localization and lower powers for nonlinear functionality. Here, we present the first experimental observations of bright polariton solitons in a strongly coupled semiconductor microcavity. The polariton solitons are shown to be micrometre-scale localized non-diffracting wave packets with a corresponding broad spectrum in momentum space. Unlike the solitons known in Bose condensed atomic gases, they are non-equilibrium and rely on a balance between losses and external pumping. Microcavity polariton solitons are excited on picosecond timescales, and thus have further benefits for information processing over light-only solitons in semiconductor cavity lasers, which have nanosecond response times.

Main

Non-spreading localized wave packets or solitons occur in a variety of nonlinear classical and quantum photonic and matter-wave situations, where they reflect the distinct physical properties of the system under consideration. Light-only solitons have been observed¹ and most actively researched in optical fibres^2,3. Fibres provide a very good experimental realization of the one-dimensional nonlinear Schrödinger (NLS) equation—a paradigm model in soliton physics that has simple soliton solutions shaped by opposing dispersive spreading and nonlinearity-induced self-phase modulation of optical pulses. Optical solitons have also been extensively studied in the spatial domain, where diffraction of propagating beams can be compensated by nonlinear changes in the material refractive index^2,4. Formally, anomalous group velocity dispersion is equivalent to diffraction: both require positive (self-focusing⁵) Kerr nonlinearity to form either temporal or spatial bright solitons².

Recently, matter wave solitons have been demonstrated in Bose condensed atomic gases, where the dispersive spreading of the localized wave packets induced by the kinetic energy of positive mass atoms is balanced by the attractive interatomic interaction^6,7. Interactions between the atoms used in condensation experiments are often repulsive. To create bright solitons in such cases, the effective atomic mass must be made negative, as has been demonstrated using optical lattices⁸. The same effect can be achieved for light in photonic crystals⁹. Strong exciton–photon coupling in microcavities results in an unusual and advantageous lower polariton branch dispersion exhibiting regions of either positive or negative effective mass^10,11 depending on the values of transverse momentum^10,11. The transition from positive to negative mass is associated with the point of inflection of the energy–momentum diagram (Fig. 1a). The negative mass of polaritons coupled with repulsive polariton–polariton interactions favours the formation of the bright solitons that we realize in the present work.

Figure 1: Experimental configuration and observation of soliton propagation.

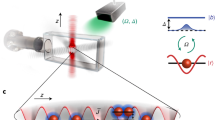
a, Dispersion (energy–momentum) diagram of the lower-branch polaritons and schematic representation of the soliton spectrum and excitation scheme. b, Schematic of soliton excitation in the microcavity structure. The c.w. pump with incident in-plane momentum parallel to the x-direction is focused into a large spot. The pulsed writing beam, also incident along x, is focused into a small spot and triggers soliton formation. c, Bistable polariton density as a function of pump momentum. Arrow indicates the state of the system created by the pump before incidence of the writing beam. d–g, Streak camera measurements of the soliton trajectories along the x-direction excited under different conditions. d,e, Components of the soliton in transverse electric (TE) and transverse magnetic (TM) polarizations, respectively. This soliton is excited with a 7-µm-wide writing beam with in-plane momentum the same as that of the pump. f, As in d, but the writing beam has half the momentum of the pump. g, As in f, but the writing beam width is 14 µm. (wb, writing beam.)

Recent discoveries made with microcavity polaritons include condensation^12,13, vortices^14,15 and superfluidity¹⁶ and follow a pathway similar to the one that led to the observation of coherent matter wave solitons^6,7. The observation of low-threshold bistability, polarization multistability^17,18,19,20 and parametric scattering²¹ of polaritons has further prepared the necessary foundations for the realization of half-light half-matter solitons. In contrast to atomic systems, polariton microcavities operate under non-equilibrium conditions. Atomic systems are typically described by conservative Hamiltonian models, such as NLS or Gross–Pitaevskii equations, whereas the polariton system is intrinsically non-Hamiltonian. In the photonic context, this system is often referred to as dissipative, which implies the importance of losses, but also implicitly assumes the presence of an external energy supply^22,23. Dissipative matter-only solitons have been considered for the exciton condensates in ref. 24, and dissipative bright polariton (half-light half-matter) solitons in microcavities have been predicted in refs 25 and 26. Various versions of the conservative half-light half-matter solitonic structures have also been considered^27,28.

Observation of bright polariton solitons

Here, we report bright solitons in a GaAs semiconductor microcavity (see Methods for sample and experimental details). The point of inflection of the polariton dispersion is found at the in-plane polariton momentum k ≈ 2 µm⁻¹ (Fig. 1a), which corresponds to a group velocity of non-interacting polaritons (1/ℏ)(∂ε/∂k) ≈ 1.8 µm ps⁻¹, where ε is the polariton energy. We conduct our experiments with polaritons that have momenta above the point of inflection, where the polariton mass is negative, M = ℏ²(∂²ε/∂k²)⁻¹ ≈ −11.2 × 10⁻³⁵ kg (−1.25 × 10⁻⁴ m_e) at k ≈ 2.4 µm⁻¹. As for the lossy and pumped Gross–Pitaevskii equations²⁹, reasonable estimates of the non-equilibrium soliton parameters can be obtained from the conservative limit of the system. We can estimate the polariton soliton width for a given polariton density N using the well-known expression for the healing length of a quantum fluid . This is obtained by equating the characteristic kinetic energy K of the dispersive spreading of the wave packet with width w (K = ℏ²/(2Mw²)) to the potential energy U of the polariton–polariton repulsion (U = gN, where g ≈ 10 µeV µm⁻² is the two-body interaction coefficient). For the typical soliton potential energies realized in our experiment U ≈ 0.3 meV (corresponding to N ≈ 30 µm⁻²), from which we deduce w ≈ 2 µm. The short free polariton lifetime (∼5 ps) means that solitons emerging from this balance will traverse distances of ∼10 µm before they dissipate. To sustain these solitons for longer we need to provide a continuous supply of energy. Energy is pumped into the microcavity using a continuous-wave (c.w.) pump beam, focused to a 70 µm (full-width at half maximum, FWHM) Gaussian spot (Fig. 1b).

We highlight the important properties of dissipative solitons that justify the choice of our experimental parameters to realize soliton production. The polariton density varies strongly across the bright soliton profile, reaching its maximum at the centre, whereas the pump beam profile tends to hold the density at a quasi-constant level across the much larger pump spot^25,26. Furthermore, due to localization in real space the soliton profile in momentum space is broad. As a result, solitons can only be expected under conditions when the pump state is unstable with respect to spatially inhomogeneous perturbations at momenta different from that of the pump^25,26. If the microcavity is driven by a pump beam slightly blueshifted with respect to the unperturbed lower polariton (LP) branch, the pump polariton field exhibits bistability as a function of the pump beam power and angle (Figs 1c, 4). The polariton bistability is usually accompanied by parametric (modulational) instability, which has been studied extensively in microcavities^17,30,31. This instability is a particular case of polaritonic four-wave mixing. Bright solitons are excited on top of the stable background of the lower branch of the bistability loop (Fig. 1c) and can be qualitatively interpreted as locally excited islands of the modulationally unstable upper branch solution^25,26. Broadband four-wave mixing of polaritons, expanding well beyond the momenta intervals with the parametric amplification, enables coherent scattering from the locally perturbed pump to the continuum of momenta forming the soliton (Fig. 1a). Simultaneously, the soliton formation requires the transverse momentum of the pump k_p (that is, the incident angle of the laser beam) to be such that the effective polariton mass is negative, ensuring self-focusing of the repulsively interacting polaritons²⁵. This mechanism can lead to self-localization only along the direction of the pump momentum (one-dimensional solitons)²⁵. Simultaneous localization in two dimensions involves more subtle physics, and the corresponding solitons exist only in a narrow range of pump intensities²⁶.

Figure 4: Numerical modelling.

a–d, Numerically computed ideal solitons (a,b) and dynamics of the soliton excitation (c,d). In a, the full green line shows the bistable spatially homogeneous polariton state. The full black line and the dashed red line show the amplitudes of the TE (E_TE) and TM (E_TM) components of the elliptically polarized soliton, respectively. b, Spatial profiles of the TE (full black) and TM (dashed red) soliton components. Inset: soliton profile when the light with k_x ≥ k_p has been filtered out. c,d, Dynamics of the soliton width and peak intensity as functions of position across the microcavity. The writing beam is 7 µm wide and its duration is 1 ps. Different line colours correspond to the different intensities of the writing beam indicated in d. One unit of all the plotted dimensionless field amplitudes corresponds to the pump beam amplitude E_p at the right end of the lower branch of the bistability loop (see a).

Figure 1c shows the bistable dependence of the polariton emission intensity collected from our device at nearly zero transverse momenta (direction normal to the cavity plane) as a function of the pump momentum (k_p) at the fixed energy of the pump photon 1.5363 eV, which is ∼0.3 meV above the unperturbed LP branch at k_p ≈ 2.37 µm⁻¹. With k_p increasing beyond the bistable interval, the intracavity polariton field increases abruptly over the excitation pump spot. This transition is also accompanied by the strong parametric generation of polaritons into the state with k ≈ 0 (refs 17,21). According to the above discussion and the predictions of refs 25 and 26, bright polariton solitons should exist within the bistability interval (Fig. 1c).

We excited bright polariton solitons using a picosecond writing beam focused into a spot (Fig. 1b) with a diameter in the range 7–15 µm, which is small compared to the diameter of the pump beam of 70 µm. The writing beam was TE-polarized and the pump beam TM-polarized. The experimental arrangement of the pump and writing beams is shown schematically in Fig. 1b, with both beams incident along the x-direction. The unperturbed polariton density (before the application of the writing beam) was in the state corresponding to the lower branch of the bistability loop (see arrow in Fig. 1c), with no indication of the parametric generation of polaritons with momenta different from the pump. The bistability domain was scanned by changing the pump momentum, and it was found that the optimal conditions for clear soliton observations existed close to the right boundary of the bistability interval shown in Fig. 1c. The solitonic emission was collected along a 2-μm-stripe of the streak camera image (see Methods) parallel to the direction of incidence of the pump. The light was collected inside the finite interval of angles corresponding to momenta 0 < k_x < k_p, thereby avoiding collection of the reflected pump beam, which otherwise leads to detector saturation. Figure 1d,e shows spatiotemporal traces of the intensities in TE and TM polarizations for typical non-diffracting and non-decaying propagating wave packets excited with the writing beam. Here, the 7 µm writing beam arrives at position x = −20 µm at time t = 0, where the writing beam transverse momentum is the same as that of the pump k_wb = k_p.

We now present the experimental results, supported by theory in the next section, which prove that the wave packets arise from bright polariton solitons propagating across the excitation spot. We first demonstrate that the velocity of the soliton is independent of k_wb. The role of the writing beam is to create a local perturbation of the pump state, which in turn results in soliton formation due to scattering from the pump state (Fig. 1b). It has been shown numerically for linearly polarized polariton solitons that their velocity is close to the group velocity of the polaritons at the pump momentum²⁵. To test this prediction, we changed the momentum of the writing beam to half of the pump momentum, k_wb = k_p/2 (Fig. 1f,g). We observe a soliton velocity in Fig. 1f of ∼1.68 µm ps⁻¹, the same as that in Fig. 1d,e, where k_wb = k_p. The independence of the polariton soliton velocity on k_wb is in sharp contrast to that expected for conservative solitons, where the soliton velocity is solely determined by the momentum of the excitation pulse².

We also show that the size of the soliton is determined by the pump and cavity parameters and is independent of the size of the writing beam, as is true for other types of dissipative solitons^22,23. The size of the excited wave packet, w, in the soliton regime is expected to be fixed by the potential energy U of the solitons, where U is of the order of the pump energy detuning with respect to the energy of the unperturbed lower branch polaritons ( as discussed earlier). This is illustrated in Fig. 2a–f, which shows the profiles of polariton wave packets along their propagation direction (x) at different times and positions for writing beam sizes of ∼7 µm (Fig. 2a–c) and ∼15 µm (Fig. 2d–f). In the initial stage of soliton excitation, these writing beams produce polariton wave packets of very different widths (Fig. 2a,d), which then quickly evolve into solitons of the same size (∼5 µm), as shown in Fig. 2b,e, as expected for soliton formation.

Figure 2: Soliton stability.

a–c, Experimentally measured spatial intensity profiles of a soliton created by the 7 µm writing beam at different times, showing excitation and decay of the soliton. d–f, Intensity profiles of a soliton created by the 15 µm writing beam. g,h, Dynamics of the peak intensity and width of the wave packets excited by the 7 µm writing beams with different powers as they propagate across the cavity. The writing powers where the above parameters remain quasi-constant in the interval of 20–40 µm correspond to the formation of solitons. Error bars in h indicate the standard deviation of measurements.

We next demonstrate the unambiguous non-spreading and non-decaying features of the soliton wave packets. Figure 2g,h shows the dependences of the intensity and width of the excited wave packets, respectively, on their position as a function of the writing beam power, P_wb. Within the range of P_wb from 1.6 mW to 2.3 mW, the soliton intensity and width are nearly constant. Furthermore, the width versus position dependence (Fig. 2h) exhibits a plateau in the interval ∼20–40 µm. These signatures of polariton soliton formation are further discussed in the section on modelling. There is a transient region from 5 to 15 µm where a soliton of small size builds up (Fig. 2h), while the polaritons initially excited by the writing beam decay. The size of the transient region is probably determined by the free polariton propagation length of ∼10 µm. At the edge of the pump spot, the pump intensity is insufficient to maintain the system within the bistability region and thus to sustain solitons. This is the main factor determining the practical extent of the soliton trajectory, and leads to spreading and dissipation of the excited wave packets at times greater than 40–45 ps when the edge of the pump spot is approached, as shown in Fig. 1d–g and Fig. 2c,f.

We note that the intensity of the writing beam must be high enough to enable soliton switching (Fig. 2h). As one reduces the writing beam intensity below the threshold of 1.3 mW (Fig. 2h) for soliton switching, we observe an abrupt decrease in the intensity and an increase in width of the wave packet. On further reducing the writing beam intensity to P_wb < 1 mW, only quickly decaying non-solitonic wave packets are excited. For the pump momenta that are below the point of inflection, the writing beam triggers switching of the whole pump spot¹⁸ and no soliton formation is observed.

Figure 3 presents two-dimensional images of solitons. The soliton size along the y-coordinate perpendicular to the propagation direction (Fig. 1b) at 30–40 ps is ∼5 µm, narrower than the initial beam size. This indicates suppression of diffraction and localization in the direction where polaritons have a positive effective mass. Whereas localization in the x-direction described above arises from the interplay between the negative effective mass and repulsive interactions, the origin of localization along y is different. It can be interpreted in terms of the phase-dependent parametric nonlinearity and the interaction of propagating fronts²⁶.

Figure 3: Two-dimensional soliton images.

Two-dimensional streak camera measurements of a soliton travelling across the microcavity plane. Experimental conditions are as in Fig. 2a–c. Cross-sections taken along the y-direction indicate a soliton FWHM of 5 µm.

We note that our observations have a very different physical origin to the triggered optical parametric oscillator observations of ref. 32. In that case, the system was already in a high-density phase before a writing beam was applied and, furthermore, the system was pumped at low k_p in the region of positive effective mass, where soliton generation cannot occur. As a result, propagating excitations of the polaritonic condensate were studied, as opposed to the bright solitons reported here (see Supplementary Information for further discussion).

Numerical modelling of soliton formation

To provide further insight into our experimental observations, we performed a series of numerical simulations. This is important, because the previous theoretical studies of polariton solitons^25,26 are restricted to the linearly polarized case, whereas in the present setting, with orthogonally polarized pump and writing beams, coupling between the two polarizations is important and leads to the formation of elliptically polarized solitons. The model we have used includes equations for the TE-(polarization parallel to the cavity plane) and TM-polarized optical modes and for the respective excitonic fields (see Methods for details).

Transforming from the laboratory frame to the frame moving with an unknown velocity, which is consistently determined together with the soliton profile²⁵, we have found branches of elliptically polarized solitons (Fig. 4a,b). These solutions retain their spatial profile and all other characteristics for indefinitely long times. The soliton branches with positive slope in Fig. 4a represent propagating solutions, which are stable with respect to perturbations. The negatively sloped branches correspond to unstable solitons. These ideal solitons have been calculated on top of the spatially homogeneous pump and move with velocities of ∼1.7 µm ps⁻¹, in good agreement with experiment.

Another series of numerical simulations was conducted to demonstrate the excitation of solitons with 1 ps pulses on top of the Gaussian pump beam (Fig. 4c,d). Figure 4c (cf. Fig. 2g) and Fig. 4d (cf. Fig. 2h) show changes of the peak intensity and of the width of wave packets travelling across the microcavity for several intensities of the writing beam. The saturation of both parameters with increasing intensity of the writing beam (Fig. 4c) as well as the quasi-constant soliton width in the region from 5 µm to 30 µm of the propagation length (Fig. 4d) demonstrate the transition to the soliton regime, which is fully consistent with the experimental observations in Fig. 2g,h. The observed saturation behaviour indicates that, as for other dissipative solitons^22,23, the soliton width in our case is fixed by the pump and cavity parameters^25,26 and not by the writing beam powers. This is in strong contrast to conservative solitons, which for the given system parameters can exist with an arbitrary width determined by the density N initially induced by the writing beam.

Soliton observation in energy–momentum space

The soliton formation can also be viewed as scattering of pump polaritons into a continuum spanning a broad range of transverse momenta from 0 to 2k_p (Fig. 1a)²⁵. Our measurements of the energy–momentum (E(k_x)) profile of the solitonic wave packets over time (Fig. 5) confirm this point. Initially, for t < 20 ps, the polariton emission is concentrated mostly close to k_p, whereas at later times (30–40 ps) the emission is distributed over a broad range of momenta, a characteristic feature of soliton formation²⁵. The soliton spectra are expected to form a straight line tangential to the dispersion of non-solitonic radiation^3,25. Indeed, the measured dispersion at 30–40 ps can be approximated by a straight line (dashed lines in Fig. 5b,c) in agreement with our numerical modelling (Fig. 5k,m). We note, however, that soliton emission forms at k-vectors k_x ≥ 0.5 µm⁻¹ and spans over the point of inflection, where the dispersion of non-interacting polaritons is also close to linear. Nevertheless, the difference between the solitonic dispersion observed in the experiment at ∼30–40 ps (in modelling at 13–27 ps) and the dispersion of the non-solitonic polaritons observed at later times ≥50 ps (in modelling at 27–40 ps) is clear from the data shown in Fig. 5. The soliton velocity, (1/ℏ)(∂ε/∂k_x), deduced from the dashed lines in Fig. 5b,c is ∼1.6 µm ps⁻¹, consistent with the measurements in Fig. 1 and the numerical modelling. The difference between the experimental TE and TM emission in momentum space may arise from anisotropy of polariton scattering dynamics³³, which is not taken into account in our modelling.

Figure 5: Soliton spectra.

Images of polariton emission in energy–momentum space taken at different times after the application of the writing beam in TM (bottom panel) and TE (top panel) polarizations. a–j, Experimental data. Dashed line is a linear fit to the experimental measurements. The energy resolution of 0.1 meV limits the time resolution to ∼10 ps. k–n, Numerical simulations of polariton emission in time intervals of 13–27 ps (k,m) and 27–40 ps (l,n) after application of the writing beam. Note that the span in the momentum space is wider than in the experimental figure. Dashed lines show the LP branch.

Discussion and conclusions

The experimental observations of bright polariton solitons reported here should pave the way to the investigation of a number of phenomena of fundamental significance, such as interactions between solitons with different spins and the formation of soliton molecules. It is also notable that the number of polaritons in the solitons observed is of the order of hundreds, which puts them into the category of mesoscopic structures. The realization of spatially modulated one-dimensional microcavity structures, for example, with reduced numbers of particles may thus create conditions for the observation of quantum and discrete solitons. We note also that, unlike the well-studied polariton condensates, which correspond to macroscopic occupation of a single state in momentum space, the highly occupied polariton soliton is strongly localized in real space with a broad spread in energy and momentum.

The observed polariton soliton can be useful for potential applications in ultrafast information processing, because their picosecond response time is three orders of magnitude faster than that observed for the pure light cavity solitons in the wide-aperture semiconductor lasers (VCSELs)^23,34,35. Furthermore, polaritonic nonlinearities are 2–3 orders of magnitude larger than nonlinearities in VCSELs^23,34,35. The measured transverse dimensions of polaritonic solitons are ∼5 µm, which is resolution-limited. The real soliton size can be smaller, because the numerical model using the experimental parameters predicts ∼2 µm, several times less than the 10 µm width typical for VCSEL solitons. Polariton solitons can potentially be used as more natural information bits than the propagating domain walls in the recently proposed integrated polariton optical circuits and gates (polariton neurons)³⁶. Furthermore, nonlinear functionality relying on few polariton quanta allows the design of quantum polariton–soliton circuits. For practical applications, solitons will have to be investigated in materials where strong coupling persists at room temperature, such as in GaN³⁷ or ZnO microcavities or high-quality GaAs microcavities with a large number of quantum wells³⁸.

In parallel with our work, Amo and colleagues have very recently reported observations of dark one-dimensional polariton solitons³⁹. These solitons are formed by polaritons with positive mass in collision with obstacles. A most important physical difference with the bright polariton solitons reported here arises from the fact that in the experiment of ref. 39, the solitons are observed outside the pump spot, necessary to avoid locking of the dark soliton phase to the pump phase in their one-beam experiments. Such an arrangement selects conservative solitons propagating in the presence of the unbalanced absorption.

Methods

We used a GaAs-based device with six 15-nm-thick quantum wells grown by molecular beam epitaxy. The experiments were performed at a temperature of 5 K. Propagation of the wave packets in real time was recorded using a Hamamatsu streak camera with a time resolution of 2 ps. An aspheric lens with a focal length of 4 cm and numerical aperture NA = 0.44 provided optical resolution of ∼4–5 µm for both soliton excitation and imaging. Two-dimensional images of solitons at different times were reconstructed from an array of one-dimensional images versus position x such as in Fig. 1, obtained at different positions y on the pump spot. Solitons were driven by a TM-polarized c.w. pump beam and triggered by a pulsed TE-polarized writing beam with duration of 5 ps. The pump and writing beams were directed to the microcavity through the same optical path using a polarizing beamsplitter. The orthogonal polarizations of the beams were chosen to ensure transmission of maximum available powers from each of the lasers to the sample.

Numerical studies were performed using mean-field equations describing the evolution of slowly varying amplitudes of the TM (E_TM) and TE (E_TE) cavity modes and of the corresponding excitonic fields ψ_TM,TE:

Here, m_c = 0.27 × 10⁻³⁴ kg is the effective cavity photon mass, ℏΩ_R = 4.9867 meV is the Rabi splitting, ℏ γ_c = ℏ γ_e = 0.2 meV, where γ_c and γ_e are the cavity photon and the exciton coherence decay rates, δ_e = −1.84 meV, δ_c = −2.34 meV, g > 0 is the nonlinear parameter, which can be easily scaled away, and r = −0.05 parameterizes the nonlinear interaction between the two modes⁴⁰. E_p(x, y) is the pump amplitude with momentum k_p, the corresponding angle of incidence is θ = arcsin[k_pλ_p/(2π)] and E_wb is the writing beam amplitude.

For the case of the homogeneous pump, E_p(x, y) = const. and E_wb(x, y, t) ≡ 0, and the soliton solutions are sought in the form E_TM,TE = A_TM,TE(x − vt)$e^{i{k}_{\text{p}}x}$, ψ_TM,TE = Q_TM,TE(x − vt)$e^{i{k}_{\text{p}}x}$. The soliton profiles and the unknown velocity v are found self-consistently using Newton–Raphson iterations. In our simulations of the soliton excitation, the system of equations (1) to (4) was solved directly using the split-step method.