Main

The construction of a universal quantum computer that is capable of implementing any quantum computation or quantum simulation1 is a major long-term experimental objective2. However, non-universal quantum machines, which exploit characteristics of their own physical system to solve specific problems, could outperform classical computers in the near term3. Ensembles of single photons in linear optical circuits have recently been proposed4. Despite being non-interacting particles, their detection statistics are described by functions that are intractable to classical computers—matrix permanents5,6,7,8. It is therefore believed that linear optics could constitute a platform for the efficient sampling of probability distributions that cannot be simulated by classical computers, with strong evidence provided in the case of circuits described by large random matrices4.

A universal quantum computer running, for example, Shor's factoring algorithm9 creates an exponentially large probability distribution with individual peaks at highly regular intervals, which facilitate the solution to the factoring problem. The solution can be efficiently verified classically, as is the case for all problems in the non-deterministic polynomial-time (NP) complexity class10. Accordingly, correct operation of the quantum computer is confirmed. In contrast, it is not clear that a similarly useful structure exists in the exponentially large probability distribution that is sampled when photons are detected after a random transformation. Furthermore, because such boson sampling problems4,11,12,13,14 are related to the harder #P complexity class5, it is not understood how to verify correct operation for large versions of a boson sampling machine, with formal verification likely to be classically intractable.

Experimental approach to verification

The correct operation of Shor's algorithm is verified independently of the physical platform of the universal quantum computer on which it is run. However, boson sampling is native to linear optical experiments, allowing us to exploit experimental methods and the fundamental properties of linear optics to develop procedures that provide strong evidence that the system is functioning properly. First, we are interested in finding configurations of optical circuits that engender large-scale, ordered, photonic quantum interference, to produce a predictable structure in the probability distribution of possible detection events. Fully reconfigurable circuits, capable of implementing any unitary transformation on optical modes, are realizable with arrays of beamsplitters and phase shifters15, which have been demonstrated on partially reconfigurable waveguide circuits16,17. With large-scale single-photon and multiphoton interference verified with predictable multimode correlations in a fully characterized circuit18, a reasonable assumption is that quantum mechanics holds and the system maintains correct operation as the circuit is continuously reconfigured to implement a random unitary operation.

Second, we determine that the most likely route to incorrect operation is the unwanted introduction of distinguishably between photons, which destroys quantum interference19. This effectively pushes the matrix description of the optical circuit from one with complex entries to a real-valued matrix, where classical algorithms can efficiently and precisely approximate matrix permanents corresponding to the classical probability of individual outcomes20. This regime is readily accessible experimentally, for example by introducing temporal delay between photons. The opportunity then exists to tune between ideally indistinguishable (quantum) and perfectly distinguishable (classical) data and measure the change in a suitably constructed metric. Our experimentally informed approach is different to a recently proposed test to confirm that boson sampling statistics are not drawn from an unbiased probability distribution21, which we also demonstrate, but which has the drawback that it does not distinguish between quantum and classical statistics.

In these experiments, we observe and exploit a regular structure in the quantum probability distribution generated by a circuit of continuously coupled waveguides, which arises from a phenomenon related to boson bunching, which we term ‘bosonic clouding’. This describes the increased tendency of indistinguishable photons to cluster in different but nearby modes, in a superposition around two separate locations, when compared to distinguishable photons. This has been observed for quantum walks of two photons propagating in continuously coupled waveguides22,23,24,25 and in circuits composed of arrays of directional couplers and phase shifters with ordered values26.

Here, we experimentally observe that bosonic clouding persists for systems of three, four and five photons, propagating in continuously coupled waveguides. Although the five-photon statistics arise from a partially mixed input state of five photons across four modes, the indistinguishability of the photons leads to clouding behaviour after only a low number of events. We observe the expected dissipation of bosonic clouds when distinguishability is introduced among the photons. In contrast, for circuits described by random unitary matrices, no clouding is observed for three photons. Our observation of this basic behaviour of particles is of fundamental interest; moreover, the emergence of bosonic clouds provides a way to predict multimode correlations in the transition from the classical to the quantum regime without having to calculate the matrix permanents that describe the relative probabilities for the multimode detection events.

We experimentally implemented our verification methods with three-, four- and five-photon ensembles propagating in arrays of 21 continuously coupled waveguides. The >50,000-dimensional Hilbert space accessed by a relatively low number of five-photon events exemplifies the enormity of the challenge faced by verification techniques as experiments grow in size and complexity. The computational complexity of regularly structured probability distributions arising from such systems is not known; however, for random unitary devices, strong evidence exists that efficient classical simulation is impossible4. Turning our attention to photonic networks described by random unitary matrices, we observe probability distributions with little or no apparent structure for three photons propagating in nine randomly connected optical modes, and we experimentally test the verification procedures that rule out sampling from a flat probability distribution21.

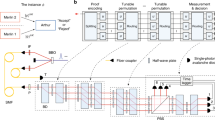
All experiments presented here use a similar set-up, as shown in Fig. 1, where multiple pairs of identical 780 nm photons are generated across four modes of a pulsed spontaneous parametric downconversion source and injected into one of two waveguide circuits, which we label QW (quantum walk) and RU (random unitary). (See Methods for experimental details and Supplementary Section 1 for a description of the three-, four- and five-photon state preparation.) The QW chip is a planar array of 21 evanescently coupled single-mode waveguides fabricated in silicon oxynitride (SiOxNy), with a circuit configuration similar to that used previously for photonic quantum walks of two photons. The RU chip is a nine-mode array of directional couplers and fixed phase shifts in silicon nitride (Si2N3), which can be fabricated to implement any fixed unitary operation15. Here we have chosen a 9 × 9 Haar random unitary matrix where coupling and phase values are effectively randomized. Detection is performed over a simultaneous maximum of 16 modes with 16 single-photon avalanche diodes (SPADs) and a 16-channel time-correlated single-photon-counting (TCSPC) system to monitor, in real time, all ways in which p photons can be found at p of 16 detectors.

Figure 1: Experimental set-up to generate interfere and detect single photons.
figure 1

a–c, Photons generated in a pulsed spontaneous parametric downconversion source are injected, via a V-groove fibre array, to either the QW chip (b) or the RU chip (c). d, Outgoing photons are coupled from the chip using a second fibre array, either directly (not shown) to 16 single-photon avalanche diodes (SPADs), or via a network of fibre splitters (shown). Detection events are recorded with a 16-channel time-correlated single-photon counting system (TCSPC). (See Methods for a detailed description of the experimental set-up and legend abbreviations.)

Full size image

Sampling a non-trivial probability distribution

Our first experimental demonstration is motivated by the claim that boson sampling with an optical network described by a random unitary matrix is operationally indistinguishable from the case where detection events are drawn from an unbiased or flat probability distribution, with discrimination between the two only becoming possible after an exponential number of trials27. We experimentally implemented a procedure that—reasonably—uses knowledge of the unitary operation to efficiently verify that detection statistics are not collected from a flat probability distribution21. (Note that, even if the unitary description is a priori unknown, it can be efficiently measured; for example, see ref. 28.) The theoretical discriminator R* is the product of squared row 2-norms of the p × p sub-matrix M, which describes a transformation of p photons, and is calculated from the complex matrix elements {ai,j} by computing, for each row, Ri = |ai,l|2 + |ai,2|2 + ··· + |ai,p|2, then taking the product and normalizing so that E[R*] = 1. Intuitively, this discriminator works because R* is sufficiently correlated with |Per(M)|2, the probability of detecting p photons in p modes (a p-fold detection), given by the mod square permanent of the transformation sub-matrix.

We collected 434 threefold detections after injecting p = 3 photon states into our m = 9 mode RU chip, shown in Fig. 1c, the unitary matrix description for which was reconstructed from single-photon and two-photon tomography28. Figure 2a shows a histogram of R* for these 434 events, together with numerical plots for both bosonic () and flat () distributions obtained by averaging over 1 × 105 Haar random unitaries. To quantify the performance of this discriminator, we use Bayesian model comparison to update, in real time, our relative confidence that the samples were drawn from rather than . Figure 2b shows that, after only 12 threefold detection events, a confidence level of 90% that sampling is not from is achieved, which rises to 1–10−35 by the end of the experiment. (See Supplementary Section 2 for details of this calculation.)

Figure 2: Three-photon data from the RU chip showing verification of boson sampling against the uniform distribution and discrimination between quantum and classical statistics.
figure 2

a, The expected PDF for values of R* for submatrices chosen from the boson sampling distribution (blue line) and the uniform distribution (black line). The bars show a histogram of R* values from the experimental three-photon data. b, Dynamic updating using the Bayesian model comparison for confidence in sampling from the boson sampling distribution, rather than the uniform distribution. After only 12 threefold detection events we are over 90% confident, and by the end of our experiment we assign only 10−35 probability to the null hypothesis. c, Probability of finding p photons at p detectors (that is, no bunching) for quantum (blue) and classical (red) particles. Lines are theoretical asymptotic values with the constraint m = p2, and histograms (inset) are for theoretically simulated data for up to five photons in 25 modes. Values calculated from our experimental data are shown by the circles in the histograms for three photons in nine modes.

Full size image

Sampling a non-classical probability distribution

A more physically relevant probability distribution to rule out, which is classically simulatable21, is that which is generated when photons become distinguishable, which we label as . While R* discriminates between and , it does not discriminate between and . Indistinguishability among photons may be verified at source19, yet the circuit may introduce distinguishability through decoherence, dispersion and other extra unwanted degrees of freedom such as polarization. We therefore implement a scalable method to verify that photon indistinguishability is maintained during propagation through the circuit, based around the following question: given a p-photon input state in p modes (one photon per mode), what is the probability P(p) of finding p photons at p detectors (that is, no photon bunching)? Again, we refer to this as a p-fold detection.

The intuition that p-fold detection is less likely for indistinguishable photons due to bosonic bunching is formalized in ref. 29. A simple counting argument is used to show that, when averaged over the Haar measure for the case of p indistinguishable photons in m modes, , whereas for the case of distinguishable photons, , as in the classical ‘birthday paradox’. If m ≫ p2, then PC (p) ≈ PQ(p); however, if m = p2 then PC(p) > PQ(p), as can be seen in Fig. 2c30.

The protocol requires N trials of p-photon input states, which gives rise to M p-fold detections, allowing the comparison M/N to the analytic values of PQ(p) and PC(p). Due to the non-deterministic nature of the downconversion process, we use the method of ref. 30 to calculate P(p). Maximizing the indistinguishability of photons, we found PQ(p) = 0.450 ± 0.028, rather than the expected value of 0.509, while the deliberate introduction of (temporal) distinguishability among photons gave PC(p) = 0.680 ± 0.0002 (compared to an expected value of 0.691). Using the numerically determined probability density functions (PDFs, shown in Fig. 2c), we estimate the probability (over Haar-random unitaries) that quantum data are the result of distinguishable particles to be 3 × 10−3, while the probability that classical data are the result of indistinguishable particles is 2 × 10−2.

Introducing predictable quantum correlations

Taken together, the tests in Fig. 2 provide circumstantial evidence that a boson sampling machine is operating according to the laws of quantum mechanics21, with non-trivial dependence on circuit parameters, and is exhibiting quantum interference. However, we now present a method that provides even stronger evidence for correct operation. Consider implementing a highly structured unitary that promotes all of the essential physical features of boson sampling, including single-photon and large-scale multimode multiphoton interference, but where significantly large parts of the probability distribution of p-fold detections can be determined efficiently, classically, without calculating matrix permanents. After experimentally confirming correct multimode correlations, the optical circuit is continuously tuned to realize a unitary operation, such as a Haar random unitary, with classically intractable matrix permanents that produce classically unpredictable multimode correlations. The reasonable assumption is that correct operation is maintained during the tuning. Such a protocol could be realized by highly reconfigurable circuitry15,17. In our proof-of-principle experimental demonstration—at the classically tractable scale where correct sampling from both probability distributions can be verified—we physically swap between circuits.

The structured unitary operation we choose is our QW chip of continuously coupled waveguides22, which exhibits bosonic clouding. This effect describes an increased tendency for multimode correlations with indistinguishable particles clustering, in superposition, around two separate local groups of modes, when compared with distinguishable particles. We first observed the effect for the three-particle case, injecting three photons into the middle (j = 10, 11, 12) waveguides of the 21-mode QW chip (Fig. 1c). There are 1,771 possible three-photon detection patterns, including cases with more than one photon at a single detector; that is, bunching cases. We measured 524 of the 1,771 possibilities, including some of the bunching cases, by using fibre splitters and multiple detectors to achieve non-deterministic number-resolved photon detection. (See Supplementary Section 3 for further details on data analysis.)

The large number of three-photon detection events is sufficient to reconstruct the QW chip probability distributions from which they are drawn. These are shown in Fig. 3c,d,g,h for both indistinguishable and distinguishable (temporally delayed) photons, together with theoretical models. We found a statistical fidelity between the normalized theoretical and experimental probability distributions of FQ = 0.930 ± 0.003 and FC = 0.961 ± 0.002 for the indistinguishable and distinguishable cases, respectively. Error bars were calculated by propagating Poissonian count rate errors. The deviation from unit fidelity can be attributed to unwanted temporal distinguishability among photons31, instances of photon numbers greater than three (which occur with a small probability in the photon generation process) and other experimental imperfections. For the theory model, by assuming a nearest-neighbour Hamiltonian32, single-photon measurements are sufficient to yield the unitary description of the circuit.

Figure 3: The absence and emergence of multimode correlations in the form of bosonic clouds in three-photon correlation cubes for a nine-mode RU and a 21-mode QW.
figure 3

The radii of spheres centred at coordinates (i, j, k) are proportional to the probability of finding three photons in output modes i, j and k, respectively. a,b, We tune between indistinguishable (blue) and distinguishable (red) photons by introducing a time delay between them. These data represent an experimental nine-mode RU with indistinguishable (a) and distinguishable (b) photons. c,d, Bosonic clouds from an experimental 21-mode QW unitary with indistinguishable (c) and distinguishable (d) photons. e,f, Theoretical nine-mode RU with indistinguishable (e) and distinguishable (f) photons. g,h, Theoretical bosonic clouds from 21-mode QW unitary with indistinguishable (g) and distinguishable (h) photons. The experimental data (top row) have been corrected for detector efficiencies and the theory has been filtered to show only events that were experimentally measured, which is the main reason for the apparent asymmetry between the pair of boson clouds.

Full size image

Bosonic clouding behaviour can be clearly seen for indistinguishable photons in Fig. 3c. Here, photons cluster around the main diagonal line of the correlation cube, where probabilities exactly on this line correspond to full bunching of all three photons in the same mode. Two clouds have formed at separate locations in the cube, centred on modes 6 and 16. If one photon is detected in the locality of mode 16 (for example), the remaining two photons have a higher probability of being correlated to this event and also detected around mode 16. In contrast, when temporal distinguishability is introduced between all photons (Fig. 3d), quantum interference is destroyed and the clouds dissipate; there is now a higher probability that the two remaining photons will be found away from the modes local to mode 16.

For further comparison, we have also presented all possible 84 (non-bunched) three-photon correlated detection probabilities in the RU chip in Fig. 3a,b,e,f. We note that the clouds observed in Fig. 3c are absent in the RU chip for both indistinguishable (Fig. 3a) and distinguishable photons (Fig. 3b), and the correlation cubes do not reveal any discernible structure. Here, we found a fidelity between our experiment and the theoretical model of FQ = 0.939 ± 0.010 and FC = 0.970 ± 0.007, for indistinguishable and distinguishable photons, respectively.

The bosonic clouding observed for three photons in the QW chip persists for higher numbers of photons. This allows the construction of a metric that can efficiently confirm multimode correlations consistent with probabilities determined by matrix permanents. The metric works by assigning a value –1 ≤ c ≤ +1 to each trial, where +1 is awarded when all p photons are found in either the upper or the lower half of the chip, –1 is awarded if exactly p/2 photons are found at both sides of the chip, and intermediate values are linearly interpolated for approximate clouding. More precisely, if t and b are the number of photons found, respectively, in the top and bottom halves of the chip, ci = 2|(t – b)/(t + b)| – 1 for the ith trial, and the clouding metric is calculated as the average over all n trials. To make our metric suitable to standard detectors that do not give information on the number of photons received, here does not include bunching terms (when more than one photon arrives at a single detector), which we expect would enhance the clouding metric. Exact numerical simulations for up to p = 7 photons in p2 modes confirm that efficiently reveals clouding, discriminating between indistinguishable and distinguishable photons. Approximate Monte Carlo numerical simulations support the efficiency of the clouding metric for up to p = 14 photons in p2 modes. (See Supplementary Section 4 for further details.)

We evaluated this metric with the data from our three-photon experiment (Fig. 3c,d,g,h) and with four- and five-photon experimental tests. In the four-photon case, our metric is evaluated for an input state of one photon per mode in the central (j = 9, 10, 11, 12) waveguides, and uses a sifting technique to remove unwanted terms of more than one photon per mode. In the five-photon case, the input state is a partial mixture of the ways in which six photons are generated from the photon sources and collected across four modes, with one photon lost before detection. (See Supplementary Section 3 for details of sifting and state generation.) The mean values of for the three-, four- and five-photon experiments are shown in Fig. 4c–f, for indistinguishable and distinguishable photons, alongside ideal theoretical distributions. Experimental imperfections result in non-ideal values of , yet the pertinent quantity, , is clearly revealed by our data.

Figure 4: Experimental verification of correct sampling with bosonic clouding using a QW unitary.
figure 4

a, Experimental data for four indistinguishable photons in a 21-mode QW, with black points showing 1,016 of the possible 10,626 detection patterns, ordered by descending theoretical probability (red points). Data circled in blue identify cases of partial or full bunching, which are not included in the clouding metrics here. Error bars are calculated from Poissonian statistics. Here, the input state includes unwanted terms with more than one photon per mode. b, Unwanted parts of the input state are sifted out, so that it approximates to one photon per mode. c–e, Results from evaluating our clouding metric for p = 3, 4, 5 photons. Experimental points with horizontal error bars are shown in blue for indistinguishable photons and in red for distinguishable photons; theoretically reconstructed distributions from the same number of samples are shown as solid lines. For three and four photons, the increase in is statistically significant. The separation is reduced for the partially mixed state of five indistinguishable photons across four modes, yet still observable with only 217 counts. In e, the theoretically predicted fall in clouding (blue dotted line) when one of the five photons becomes distinguishable is included. f, Results from the same test for three photons in a nine-mode RU. No significant levels of clouding are observed, as expected, showing that our test is sensitive to the implemented unitary. (See Supplementary Section 3 for further details on data analysis.).

Full size image

For p = 3 photons we find , compared to a numerically determined value of 0.169 ± 0.014 (Fig. 4c). For p = 4 photons we measure 1,016 out of a possible 10,626 fourfold events, as shown in Fig. 4a,b. The fidelity between experimental and theoretical probability distributions, for both indistinguishable and distinguishable photons, was found to be FQ = 0.971 ± 0.001 and FC = 0.978 ± 0.0004. We evaluated the clouding to be , compared to a numerically determined value of 0.145 ± 0.008 (Fig. 4d).

For states of p = 5 photons, where the Hilbert space of our system is >50,000 dimensions, we observed only 217 detection events. The large ratio between the number of experimental trials and Hilbert space size is representative of the challenge of verification as quantum systems grow. Our metric still found an experimental separation of compared to a numerically determined value of . These data are shown in Fig. 4e.

Clouding for three photons in the random unitary is shown for comparison in Fig. 4f, with compared to a numerical value of 0.044 ± 0.028, which is consistent with the absence of clouding.

Discussion

We have shown how to exploit the intrinsic physical properties of a quantum system, configured to a verifiable mode of operation, to assess its level of performance. A positive assessment can then be cited as evidence that the system is performing correctly when configured to an unverifiable mode of operation, such as the implementation of a quantum algorithm that is mathematically unverifiable. Here, we have demonstrated how the observation of predictable multimode correlations in the form of bosonic clouding can be used as evidence to support the existence of the multiphoton quantum interference that supports the unpredictable multimode correlations at the heart of boson sampling.

Each platform for quantum technologies will exhibit features that allow an assessment, at a physical level, of its operation in the quantum regime. For example, in fermionic systems, anti-bunching due to the Pauli exclusion principle could indicate the quality of the fermionic quantum interference essential for some higher-level quantum computation. We expect physical-level verification methods to gain greater importance as, increasingly, techniques will need to keep pace with the growing scale and complexity of quantum systems33.

Methods

Photon source

See Fig. 1 for the experimental set-up. Laser light (780 nm) from a 140 fs pulsed Ti:sapphire laser is attenuated with a half-wave plate (HWP) and polarizing beamsplitter (PBS), before frequency-doubling with a type-I β-barium borate (BBO) nonlinear crystal. The resulting 390 nm light is reflected from four dichroic mirrors (DMs) and focused onto a type-I bismuth triborate BiB3O6 (BiBO) nonlinear crystal to generate multiple pairs of photons through spontaneous parametric downconversion. After passing through an interference filter (IF), photons are reflected off prisms (PRs) and collected into four polarization-maintaining fibres (PMFs), which are butt-coupled, via a V-groove fibre array, to either the QW chip or the RU chip.

Device with nine-mode RU

The m = 9 mode random unitary was fabricated in silicon nitride (Si2N3) with a refractive index contrast . The waveguides have a width of 1.5 μm and outside the interaction region are separated by 127 μm. The device consists of 36 directional couplers such that the waveguides are brought to within 2.5 μm of one another, for an interaction length of ∼400 μm (dependent on the desired splitting ratio). The fibre-to-fibre coupling efficiency is ∼5%.

Device with 21-mode QW unitary

The m = 21 waveguide array was fabricated in silicon oxynitride (SiOxNy). The index contrast of 2.4% enables fabrication of micrometre-sized single-mode waveguides in compact circuit designs with a minimum bend radius of 560 μm. The waveguides were designed to have a constant width of 2.2 μm and height of 0.85 μm. They are pitched at 1.3 μm within the coupling region of length 700 μm to achieve sufficient mode overlap for nearest-neighbour coupling. The waveguides bend adiabatically to a pitch of 127 μm at the input and output facets to match the standard separation of the fibre arrays we butt-couple to the chip. The waveguides are tapered to a width of 0.7 μm at the facet to achieve better mode overlap with the fibre modes; this way we obtain an overall fibre-to-fibre coupling efficiency of ∼30%.

Detection scheme

Photons were detected with single-photon avalanche diodes (SPADs), which have a high probability of emitting a signal when they receive one or more photons, but the signal does not give information on the number of photons it receives. Therefore, with a standard detection scheme of one SPAD per optical mode, a p-photon coincidence is registered only if each photon occupies a different mode. However, it is possible to build an approximate photon-number-resolving detector for a particular mode in the circuit by connecting it to a cascade or tree of fibre splitters, the ends of which are each connected to a SPAD. As the size of the tree grows, so does the probability of detecting all p photons that were initially bunched into one mode.

In the context of our three-photon correlation cubes from Fig. 3, off-diagonal elements represent non-bunched, or collision-free, events where j1 ≠ j2 ≠ j3  ≠ ··· ≠ jp. Diagonal elements, where ja = jb for some a,b [1, …, p], a ≠ b give the probability of finding two or more photons in the same spatial mode and must be measured using fibre splitters and multiple detectors.

For the three-photon case in particular, correlations of the form and were measured between all even-numbered and all odd-numbered waveguides. We also measured all possible three-photon coincidences, including , across the four sets of waveguides {1–5}, {6–10}, {11–15} and {16–20}. In total we measured 524 out of a possible 1,771 threefold events.

For the four-photon case we measured collision-free events of the form across the set of 16 waveguides numbered {3–10, 12–19} and all possible four-photon coincidences across waveguides {3, 7, 11, 15}.

During the final revision of this manuscript, efficient experimental validation of photonic boson sampling against the uniform distribution has been reported online34.