Main

Coherent atom–light interactions lie at the heart of many quantum information systems1,2. In particular, implementations of quantum repeaters are likely to rely on mapping of photonic states onto atomic systems to enable storage of quantum information3. Coherent control over the propagation of light can also be used to vastly reduce the speed of light, thereby extending the interaction times attainable within an atomic medium. This is one proposed method for enhancing nonlinear photon–photon interactions to be used in deterministic quantum logic gates4.

A technique commonly used to control the propagation of light in atomic media is electromagnetically induced transparency (EIT)5. In this scheme, a pulse of probe light resonant with an ensemble of three-level Λ-type atoms may be transmitted through the atoms with the assistance of a bright control field that couples the probe field to a spinwave in the atomic ensemble. As the control field amplitude is reduced, the probe field velocity and amplitude are both reduced. In the limit where the control field is switched off, the probe field amplitude and velocity both fall to zero and the probe field is fully mapped into a stationary atomic spinwave. This is sometimes referred to as stopped light. Several experiments have shown how EIT may be used to enhance optical nonlinearity6,7,8,9.

Another form of light with reduced group velocity is stationary light (SL). This was originally proposed10 and demonstrated11,12 by adding a counter-propagating control field to regular EIT. The bi-directional control field leads to a stationary probe field that has non-zero amplitude. At first, this effect was attributed to the standing wave in the control field creating a bandgap preventing the propagation of the probe11,13. Later analysis showed that counter-propagating control fields of very different frequencies can also give rise to SL. The explanation is that shape-preserving EIT propagation in both directions can add up to prevent propagation12,14,15. In fact, true standing wave control fields can cause unwanted coupling between counter-propagating fields and additional decay of the SL pulse16,17,18,19. The behaviour of EIT stationary light is well understood20,21,22,23,24,25,26,27,28, and the interaction between SL and a stored light pulse has been demonstrated29.

In this work we present a technique where we excite an atomic spinwave that self-stabilizes to a solution that supports SL. The scheme is based on an ensemble of three-level Λ-type atoms with off-resonant driving fields (Fig. 1a). In this Raman configuration, bright counter-propagating control fields (Ω±) and weak probe fields () drive the spinwave in the atoms through a coherent scattering process. The SL states in our scheme have a nature significantly different from those observed previously using EIT. We show that there is a simple condition for the existence of SL in our system that allows for a wide range of possible spatial configurations. In particular, unlike stationary light generated with an EIT scheme, the spinwave and SL fields in our scheme can be spatially separated in the atomic medium.

Figure 1: The simplified level scheme and theoretical predictions.
figure 1

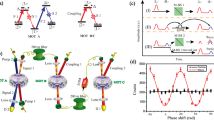
a, An energy level scheme showing how the forward (+) and backward (−) probe fields are coupled with the atoms via the forward and backward control fields. Ŝ, the spinwave, is the coherence between levels |1〉 and |2〉. b,c, Examples of stationary (b) and non-stationary (c) spinwaves at the instant the control fields are switched on. d,e, Subsequent stationary spinwave from b and non-stationary spinwave from c at time t = 5T. In b–e, Probe fields are given by the spatial integrals of the spinwave (green) in their directions of travel, forward (blue) and backward (orange) (see equations (2) and (3)). Where the two regions of spinwave have opposite phase (φ = π, b and d), the spinwave integrates to zero and does not evolve. The spinwaves at each end of the ensemble radiate probe light in both directions with opposite phase, and the light emitted by one is absorbed by the other. Where the two regions have the same phase (φ = 0, c), they emit in phase, and the probe fields escape. As the two probe fields do not cancel, the spinwave rapidly evolves until it integrates to zero as in e. In this example, the spinwaves were written using a probe pulse of amplitude 1 and duration T. The control field intensity is chosen so that the SL amplitude is equal to that of the input pulse.

Full size image

In the following section we will illustrate theoretically how an initial spinwave encoded in the atoms evolves to a state with constant spinwave and SL amplitudes. We then present experimental results that verify the existence of this self-stabilized state by directly imaging the spinwave as it evolves in the atomic ensemble and find excellent agreement with a simple model of the system. Finally, we explore what advantages our scheme may have for enhancing nonlinear interactions.

A theoretical description of self-stabilizing stationary light

The simplified atomic level scheme that we consider is illustrated in Fig. 1a. Two hyperfine states, |1〉 and |2〉, are coupled through two Raman transitions via the excited state |3〉. Each of the Raman transitions consists of a weak probe on the |1〉 →| 3〉 transition and a strong coupling field Ω± on the |2〉 → |3〉 transition, where the subscripts + and − refer to the direction of propagation. The two Raman transitions are in two-photon resonance with the |1〉 → |2〉 coherence, counter-propagate with respect to each other, and are symmetrically detuned above and below |3〉 by Δ. The symmetric detuning ensures that the dispersion experienced by each of the probe fields due to the excited state is equal and opposite, such that the two Raman transitions can be phase-matched throughout the ensemble.

The evolution of the coupled light–atom system is governed by the Maxwell–Bloch equations. We adiabatically eliminate |3〉 by assuming that Δ ≫ Γ, where Γ is the excited state linewidth, and write the simplified equations of motion as

where d is the amplitude optical depth and is the collective operator for the |1〉 → |2〉 spinwave. The rate γ is the decay of the spinwave. To understand the underlying coherent dynamics, we will ignore this decay for the time being. The derivation and assumptions necessary to obtain equations (1)–(3) are included in the Supplementary Methods.

We solve the equations of motion by integrating equations (2) and (3), take Ω+ = Ω− = Ω and substitute into equation (1) to arrive at

The right-hand side is proportional to the integral of the spinwave over the length of the ensemble, which means that the time derivative of is equal at all points in the ensemble. Consequently, the integrated spinwave amplitude will evolve at the rate d ΓΩ2/Δ2 towards a state where the integrated amplitude (and thus also the average) of is zero. During this phase of the evolution, the spinwave is being driven by the term in equation (1).

If the initial spinwave is a constant, then it will decay completely. If the initial spinwave has any spatial structure, however, what remains is a spinwave with an average of zero over the length of the ensemble. Along with this, we also have probe fields that will be confined to the atomic ensemble. To see how this works we can look at equations (2) and (3). These equations show that if the spatial integral of is zero over the whole ensemble, then the amplitudes of the probe fields drop to zero at the edge of the ensemble. In this case, inside the atomic cloud the counter-propagating probe fields have equal magnitude but drive the atoms with opposing phase. This gives rise to destructive interference that suppresses emission of the probe light from the ensemble.

Optical bright and dark states have been found in four-level schemes previously30,31. They can also be formally identified in our system and used to explain the dynamics. The multi-wave bright state is given by , which is proportional to the term identified previously in equation (1) that drives the spinwave. The optical dark state is orthogonal to and given by . This is the stationary optical field that may be trapped in the atomic ensemble. In general, an initial spinwave will give rise to some superposition of bright and dark optical states in our system when illuminated by the control fields. The bright state will drive the spinwave, causing emission of light and evolution of the spinwave until it has a mean of zero. What remains is a stable and stationary dark state in the atomic ensemble.

In our experiments we consider two initial spinwave configurations that both consist of equal amplitude Gaussian excitations at each end of the atomic ensemble, differing by a relative phase, φ. In one, the excitations have opposite phase (φ = π) and are a stationary, dark state. Figure 1b, d illustrates this stationary solution. The optical fields produced by each of the Gaussian spinwaves destructively interfere by the ends of the ensemble so that no probe field can escape the atoms. In the second example we have Gaussian excitations with equal phase (φ = 0). In this case we expect that the system will evolve as illustrated in Fig. 1c, e. The initial unstable spinwave self-stabilizes to a dark state where there is no further coherent emission of probe light. We can understand this behaviour if we consider the initial spinwave as a sum of the bright state and a dark state. The bright-state component decays, leaving only the dark state. In the experimental results presented below we observe precisely this predicted behaviour, modified only by the incoherent decay of our atoms that we ignored in this discussion.

Experimental set-up

We test the stationary solutions using a cloud of cold rubidium atoms that are confined and cooled using an elongated magneto-optical trap32. The gradient echo memory (GEM) technique33 is used to write the initial spinwaves into the |1〉 → |2〉 atomic coherence. This method has the advantage that we may precisely engineer the spatial profile of the spinwave by manipulating the spectrum of the input probe light. In GEM, a longitudinal magnetic field gradient η is applied to the ensemble so that the two-photon detuning of the Raman transition varies linearly along the length of the atom cloud. With the forward-propagating control field present, an incoming forward-propagating probe field will be coherently scattered into a spinwave excitation at a longitudinal location that is determined by the probe frequency. The spatial profile of the stored spinwave will thus be given by the spectrum of the input probe pulse34,35.

The initial spinwaves are written into the atoms by storing probe pulses that contain two carrier frequencies, each with the same Gaussian envelope. By tuning the carrier frequencies of these pulses we can excite a spinwave that has a Gaussian excitation at each end of the ensemble. The relative phase, φ, of these Gaussian excitations can be chosen by tuning the relative phase of the carrier frequencies in the probe pulse. Once an initial spinwave is written into the ensemble, the counter-propagating control fields are turned on and the theoretical predictions are tested by observing the output probe light, and by directly measuring the evolution of the spinwave via absorption imaging. Figure 2 shows the set-up of the GEM, the absorption imaging, and the additional control field and detection used for measuring stationary light.

Figure 2: The experimental schematic for the SL pulse generation in an ensemble of cold 87Rb atoms.
figure 2

The spinwave is created by storing a probe pulse via the gradient echo memory technique with forward control field (kc+). The magnetic field gradient over the ensemble is controlled by a set of coils (GEM coils). An imaging beam (resonant with |52S1/2(F = 1)〉 → |52P3/2(F′ = 2)〉) is used for the absorption imaging of the spinwave. Detector D1 measures the backwards probe field; D2 measures the forward probe field; QWP is a quarter-wave plate and PBS is a polarizing beamsplitter. Inset: The angles between the forward (backward) probe field and the forward (backward) control field are set to be θ, where the phase matching condition kp+ − kc+ = kp− − kc− = ks is satisfied. Here, ks denotes the spinwave vector.

Full size image

Experimental characterization of stationary light

We will now compare our experimental results to the simple analytic theory presented above and numerical simulations that include decoherence effects (see Supplementary Methods). Figure 3a shows the photo-detector measurements of the light that is released by the atoms (D1 and D2 in Fig. 2). Some of the input pulse, centred around 20 μs, leaks through due to the finite optical depth and is observed at D2. The ensemble is then illuminated by the dual control fields at 60 μs. For the φ = 0 case we see a large signal at D1 and D2. This signal is attributed to light released as the spinwave evolves to the stationary spinwave, as illustrated in Fig. 1c, d. Upon recall from the ensemble with the forward control beam, we observe a much smaller output for the φ = 0 case. The numerical simulation is in very good agreement with these observations.

Figure 3: Stationary light results.
figure 3

Inset (top-left) shows timing diagrams for the control fields (Ω±) and GEM gradient (η) used in the experiments in a and b. a, The forward- and backward-propagating probe fields as detected on photodiodes (top) and in simulation (bottom). Stationary light (φ = π) and non-stationary light (φ = 0). b, Top row shows the experimentally measured evolution of the spinwave. Middle row shows simulations of the spinwave. Bottom row compares experiment (green) and simulation (black line) over the z direction at a time of 70 μs. Left column shows results for a single forward control field. Middle column has counter-propagating control fields and a spinwave phase of φ = π. Right column has counter-propagating control fields and a spinwave phase of φ = 0. c, Simulations of the probe field intensities for the situations corresponding to the columns of b. Top row shows the magnitude of the forward-propagating probe field. Bottom row shows cross-sections at 70 μs with both forward (blue) and backward (yellow) probe field components.

Full size image

A more detailed picture of the dynamics is gained from the absorption imaging shown in Fig. 3b. The experimental data in (i–iii) is gathered by repeatedly running the experiment and adjusting the timing of the imaging beam to build up a picture of the spinwave evolution. The results of numerical simulations that solve the equations of motion with decay for the three-level system are shown directly underneath each experimental image. The simulations use the experimental parameters, apart from a small difference in the rephasing time which is introduced to match the experimental rephasing. Figure 3c shows the simulated optical field envelope within the ensemble, illustrating the SL that coexists with the observed spinwave, but cannot be directly measured.

Our experimental data show excellent agreement with the behaviour predicted by the simulations. The middle column of Fig. 3 shows results and simulations for a stationary spinwave, where the integrated amplitude of the initial spinwave is zero. In this case, as expected, we observe no evolution of the shape of the spinwave. When the counter-propagating control fields are turned on at 60 μs, there is only a gradual evolution due to decay. The right-hand column where the initial spinwave is not stable shows a rapid evolution to a stationary spinwave, marked by a horizontal discontinuity in the plot, in both the experimental data and simulated results.

Once the spinwaves have evolved to a steady state, they show a strong resemblance to those that we predict from the simple model. This can be seen by comparing the illustrations in Fig. 1 against the measured and simulated spinwaves in Fig. 3b; viii, ix. Although the phase cannot be measured directly, the recall and evolution are consistent with the theoretical prediction. Once the spinwave has reached a steady state in terms of shape, it continues to decay at a rate given by the control field scattering. The spinwave decay rate roughly agrees between experiment and simulation at 10 ± 1 kHz measured and 12 kHz in the simulations. We also verify that the steady-state solutions are a result of interference between the counter-propagating Raman transitions by repeating the experiment without turning on the backward control field. The left-hand column of Fig. 3b, c shows the oscillation induced in the spinwave and probe as they propagate out of the memory.

The simple model of our stationary light (as shown in Fig. 1) provides useful intuition, but not the same level of quantitative agreement as the detailed numerical simulations in Fig. 3. This is due to the incoherent absorption of the probe fields as they travel through the memory, which we ignored in the simple theory. This causes the counter-propagating probe fields to become unequal to each other throughout the memory, generating a background spinwave. This is most evident for the stationary spinwave (Fig. 3b; ii, v). Regions not containing spinwave when the counter-propagating control fields are switched on contain significant spinwave by the end of the experiment. In the limit where (dΓ/Δ) ≪ 1, the mechanism causes an additional decay of the SL field with exponent − (d Γ Ω/Δ2)2. In the simulations, this evolution is accompanied by a small amount of probe leakage. The leakage was below the experimental background noise level and is not visible in Fig. 3a. At larger single-photon detuning, Δ, this decay becomes negligible and the only important decay mechanisms are the spinwave decoherence (γ0) caused by atomic motion and ground-state dephasing and control field scattering. The equations of motion for this system approach the simplified equations (1)–(3), with a decay term γ = γ0 + 2ΓΩ2/Δ2.

Application to cross-phase modulation

It is interesting to consider how our SL scheme may perform in an implementation of cross-phase modulation (XPM), where one optical field creates an a.c.-Stark shift of an atomic level with which another optical field is interacting. As discussed in the introduction, this capability is highly appealing for quantum information processing but the effect is typically too weak to be useful if the interaction is not extended or strengthened. The XPM interaction may be strengthened by reducing the mode volume via optical fibres36,37,38, optical cavities39,40 or both41. Additionally, coherent control of the light propagation, such as EIT or SL, may extend the interaction time.

One advantage our SL scheme has with respect to XPM is the ability to engineer the spatial profile of the spinwaves, allowing better use of the available atoms. Like EIT-based schemes42,43,44, XPM in our stationary light is proportional to the optical depth, d, since it is this parameter that scales the intensity of the SL (see Supplementary Methods for details). If the spinwave and SL fields overlap, then optimizing XPM means striving for an atomic ensemble with large optical depth that occupies the smallest possible volume. The limit to atomic density in cold atomic systems is the Bose–Einstein condensate. Our system may relax the need to strive for such high density because the spinwave that generates the SL need not occupy the same volume as the SL, as shown in Fig. 1b. Using this arrangement one could optimize the strength of XPM by concentrating the SL only in the part of the atomic ensemble where the target photon to be phase-shifted is stored.

A second advantage of decoupling spinwave and SL is to control a potential source of noise. Localization of the light, and thus the interaction, with the spinwave, causes phase noise and limits the total phase shift in some multimode systems45,46. In EIT this may be avoided by allowing pulses of light to pass through each other, ensuring uniform interaction between the pulses. In our scheme, SL circulates around the stored spinwave in the centre of the atoms, also ensuring uniform interaction.

A recent experiment demonstrated an enhancement of d in an EIT scheme, where a probe photon modulated a level to which another weak pulse coupled6. Phase shifts of 13 ± 1μrad per photon were observed even though the geometry of that experiment limited the available optical depth. It is possible to achieve similar optical intensities in our cold-atom cloud as in the above-mentioned experiment, while making use of our full optical depth. We predict that phase shifts of the order of milliradians are possible. We also note that there may be further advantages gained by carefully choosing the species used to create the spinwave. The dynamics we describe may be applied to other ensemble systems; in particular, solid state, rare-earth systems have shown high optical depth47,48 and long coherence times49.

Outlook

The stationary light scheme described in our work provides a way to precisely engineer the spatial distribution of light trapped in an atomic ensemble. The essential condition required to ensure a stationary light solution is that the spinwave that traps the light spatially integrates to zero. This simple condition allows great flexibility in the way that the stationary light and spinwave are arranged in the atoms, enabling, for example, some advantages in the implementation of XPM schemes. There are many other directions that we can pursue for further investigations of our scheme. In the near future we plan to explore the addition of gain to the spinwave via four-wave mixing. This may be able to cancel out the scattering losses and generate a stable state of stationary light in the atoms, or even amplification of the stationary light. Additionally, we will investigate time reversal of the bright-state decay dynamics. We anticipate that this will allow for enhanced optical absorption of the atomic ensemble for limited optical depths, leading to applications in high-efficiency quantum memory schemes.

Methods

The atomic ensemble is a cloud of 87Rb atoms that are confined and cooled using an elongated magneto-optical trap (MOT)32. The atoms are optically pumped into the |52S1/2(F = 2, mF = −2)〉 ≡ |1〉 state. This provides an ensemble with a resonant amplitude optical depth of 200 ± 10 for the σ+-polarized transition from |1〉 to |52P1/2(F = 1, mF = −1)〉 ≡ |3〉. The three-level Λ system is then completed by a σ−-polarized transition from |52S1/2(F = 1, mF = 0)〉 ≡ |2〉 to |3〉. The SL scheme uses counter-propagating probe fields that are symmetrically detuned by ± 160 MHz about the |1〉 → |3〉 transition and corresponding control fields that are symmetrically detuned from the |2〉 → |3〉 transition. A 6 mrad phase matching angle between each probe field and its corresponding control field accounts for the 6.8 GHz frequency difference, as illustrated in Fig. 2 (inset). The particular selection of atomic levels provides a large transition strength for the σ+-polarized probe fields and ensures that the σ−-polarized control fields do not drive any transition out of |1〉, thereby eliminating four-wave mixing.

The two probe fields are mode-matched to the transverse profile of the atomic cloud with a beam waist of 110 μm, and exactly counter-propagate. The probes are measured with silicon avalanche photo-detectors (Thorlabs APD110A). The orthogonally polarized control fields are larger in diameter (3 mm) to uniformly illuminate the interaction region. The bright control fields are then filtered out using a combination of spatial and polarization filtering.

The transverse profile of the spinwave is imaged onto a charge-coupled device (CCD) camera with a laser pulse resonant with the |2〉 → |52S3/2; F = 2〉 transition. This pulse illuminates the entire atom cloud from the side, as shown in Fig. 2, and allows us to image the population of atoms in the |2〉 state. We use a large (3′′) aperture lens to image the MOT onto a CCD camera. This is aligned and focused using fluorescence from the atoms during the trapping phase of the experiment cycle. We then shine the imaging beam through the atoms at an angle that is perpendicular to the propagation axis of the probe fields. The beam illuminates the CCD camera with a shadow cast by absorption in the atomic ensemble. We infer the magnitude of the spinwave from the optical depth of its shadow,

A 4 μs imaging pulse is used. Each measurement is constructed from ten images, which are averaged to reduce shot-to-shot noise. The evolution of the spinwave is reconstructed by running the experiment repeatedly and varying the timing of the imaging light. This absorption imaging of the spinwave is similar to that done in ref. 50. Example raw and processed images are provided in the Supplementary Methods.

Data availability.

The data supporting the plots and conclusions drawn in this work are available from the corresponding author upon reasonable request.