Main

The COVID-19 pandemic has had a devastating effect on global health and economy. Since the identification of the first SARS-CoV-2 case in December 2019, 262.18 million infections have been recorded, and at least 5.22 million people have died as a result of the infection (as of December 2021)1. The increased mortality and complication rates of SARS-CoV-2 (ref. 2) compared with the mild diseases caused by seasonal coronaviruses (such as HCoV-229E3) have led to unparalleled governmental and individual-level responses to reduce the number of SARS-CoV-2 infections.

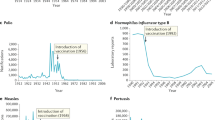
Since the beginning of the pandemic, it has become clear that many of the non-pharmaceutical interventions, such as lockdowns, are economically and socially unsustainable in the long run. Periodical loosening and tightening of social distancing measures, which present an attempt at balancing economical and sanitary considerations, have led to waves of increases and decreases in the number of SARS-CoV-2 infections per day1 (Fig. 1a). Much hope has therefore been placed on vaccine development, which would allow the immunization of a large fraction of the population, thereby substantially reducing mortality and potentially achieving herd immunity, which could in principle eradicate SARS-CoV-2 altogether. In many countries and at certain points of the pandemic, the reproductive ratio of SARS-CoV-2 has been maintained at roughly 1 (Fig. 1d), which means that the number of cases per day is on average constant.

Fig. 1: Vaccination, infection and basic reproductive ratio of SARS-CoV-2 in Brazil, France, Germany, Israel, the United Kingdom and the United States.
figure 1

a, Large-scale vaccination programmes commenced in December 2020. At the peak, Israel vaccinated more than 20,000 people per million (2%) per day. The vaccination rate decreased in April 2021 after most eligible individuals had been vaccinated. b, In an attempt to balance economic and sanitary considerations, these six countries have gone through several cycles of loosening and tightening government-imposed restrictions, resulting in periodical increases and decreases in the number of new infections per day. The Alpha variant, identified in November 2020, is most probably responsible for the increase in the number of infections in the United Kingdom and Israel at that time. The fourth wave in Israel (starting in July 2021) has been attributed to a combination of the emergence of the Delta variant and waning of immunity after vaccination. c, Vaccination in most countries follows a logistic-shaped curve. At first, priority groups are vaccinated. Then, most of the population is vaccinated in a short time frame (exponential growth). Lastly, the total number of vaccinated individuals plateaus due to vaccine hesitancy and ineligibility of the remaining non-vaccinated individuals. d, The reproductive ratio of SARS-CoV-2 infections has hovered around 1 in the six considered countries due to the imposition of non-pharmaceutical interventions to curb the infection rates. Hence, the number of infections per day has fluctuated around an average for the duration of the pandemic.

Full size image

Mass vaccination campaigns have been launched in many countries (Fig. 1b), including Israel, Germany, the United Kingdom (all with more than 60% of the population fully vaccinated) and the United States (with more than 50% of the population fully vaccinated). Currently, four companies are producing vaccines that have been approved for emergency use either by the US Food and Drug Administration4 or by the European Medicines Agency5: Pfizer-BioNTech, Moderna, AstraZeneca and Johnson & Johnson/Janssen Pharmaceuticals. Several other vaccines are also used outside of the European Union and the United States: Gamaleya (Sputnik V), Sinopharm Beijing, Sinovac, Sinopharm-Wuhan and Bharat Biotech (Covaxin)6.

However, the identification of new SARS-CoV-2 variants has cast a shadow over the expectation of a swift end of the pandemic7,8. The Alpha variant (B.1.1.7) and Beta variant (501.V2) have been shown to be neutralized to a lesser extent by convalescent and vaccinee sera9, although experiments on non-human primates have shown that this decrease might not necessarily cause a decrease in immunity10. Structural studies have mapped and predicted mutations that lead to antibody escape11,12,13. Currently, there is a discussion of whether the Omicron variant (B.1.1.529) is already such an escape mutant14. As vaccination around the world progresses, the continued evolution of SARS-CoV-2 could eventually give rise to a fully vaccine-resistant variant. Such a variant could quickly spread due to its ability to infect vaccinated and recovered people in addition to fully susceptible individuals. The question of emergence of vaccine resistance has already been the subject of many research papers15,16,17,18.

What policy would minimize the chance of emergence of vaccine-resistant strains? On one hand, policymakers can vary the extent of social distancing imposed and the regimes of vaccine administration. The critical biological parameters, on the other hand, include the infectivity of the various strains and the rate of mutation of the virus that may ultimately lead to the emergence of a resistant strain. Here we introduce a mathematical approach that examines various combinations of these parameters. Our framework helps design optimal policies that would minimize the chance of emergence of resistant strains or maximize the time until their occurrence.

Our paper is an addition to the extensive body of work that has been performed in the past year to understand the spread and evolution of SARS-CoV-2 (refs. 19,20,21,22,23,24,25). SARS-CoV-2 research has drawn on a very long history of epidemiological research26,27,28,29,30,31,32,33,34,35,36,37,38. Due to the global and urgent nature of the pandemic, many studies that could inform policymaking have been conducted25,39,40,41,42,43,44,45,46,47,48.

The probability of emergence of vaccine resistance has been studied in particular in the context of dose-sparing strategies17,18,49,50 and spatial inequalities in vaccine distribution16,51. Detailed, data-driven models for the future evolution of SARS-CoV-2, including the evolution of vaccine resistance, also exist in the literature42,52,53,54,55,56,57. However, due to their complexity, these models can be explored only by numerical simulation. In this paper, we present a simplified susceptible–infected–removed (SIR)-like model that includes dynamically adjusted social distancing measures. This feature makes the number of cases per day roughly constant on average, which allows us to derive simple formulas for the probability of emergence of vaccine resistance given the number of cases per day and the rate of vaccination.

To understand the evolutionary potential of the virus in response to a vaccination programme, we study a stochastic model for infection dynamics and virus evolution in the presence of varying degrees of social distancing and different vaccination rates. We distinguish between a wild-type virus (WT) and a vaccine-resistant mutant virus (MT). The vaccine is effective against the WT strain, while the MT strain evades immunity induced by the vaccine either partially or completely. We build on the mathematical framework of the SIR model from epidemiology35,58, albeit with considerable adjustments necessitated by the specific problem at hand. Our model keeps track of people who are susceptible, infected by WT or MT, recovered from WT or MT, and vaccinated or unvaccinated (Fig. 2).

Fig. 2: Infection dynamics, vaccination and resistance.
figure 2

Susceptible individuals (x) can be infected by WT or MT virus. Infected people (y1, y2A and y2B) die (at rate d) or recover (at rate a). People recovered from WT or vaccinated against WT can be infected by MT. People recovered from MT cannot be infected by WT. In our simplest model, we assume equal infectivity, recovery and death rates for both WT and MT. Vaccination occurs at rate c per day for all unvaccinated individuals (excluding those that are currently in active infection). Mutation happens (at rate μ) when exposure to a WT-infected individual (y1) results in the generation of an MT-infected individual. Note that when exposure to a WT-infected individual (y1) results in the generation of a WT-infected individual, the rate of infection should be multiplied by 1 − μ to conserve the sum of mutation probabilities at 1. However, since μ is small, we neglect the term 1 − μ. The rates of these events are indicated near the arrows and are used in the Gillespie algorithm implementing stochastic dynamics.

Full size image

Crucially, we assume that there is a dynamic social distancing guided by the number of new infections per day. As that number exceeds a threshold, governmental rules and individual responses reduce social activity. If the number of new infections falls below this threshold, social distancing is somewhat relaxed, and some people stop following the rules, thereby allowing higher transmission of the virus. We simulate these dynamics as a stochastic process. In consequence, we obtain fluctuating numbers of new infections per day. We introduce mass vaccination at alternative fixed rates. We then compute the probability and timing of the wave of infection caused by the spontaneous emergence of a vaccine-resistant virus.

In our approach, the mutation rate μ denotes the probability that a WT-infected individual will infect a susceptible individual with the MT strain. The exact value of this probability is currently unknown and is complex to obtain empirically. We therefore consider a wide range of mutation rates/probabilities for the simulations and calculations reported in this paper. From our model, we also derive an upper bound for the mutation rate using the fact that no wave of a vaccine-resistant variant has occurred up to now. Note that this rate can be very different from the per-base mutation rate of SARS-CoV-2, which is about 10–6.

Our model keeps track of eight different variable states: individuals who are susceptible (x), infected with WT (y1), non-vaccinated and infected with MT (y2A), vaccinated and infected with MT (y2B), recovered from WT (z1), recovered from MT (z2), vaccinated but susceptible to MT (w1), and vaccinated and recovered from MT (w2) (Fig. 2).

The WT strain can infect susceptible individuals (x), converting them to individuals infected with WT (y1) at rate β1. A mutation can occur with probability μ. In this case, a WT-infected individual infects a susceptible individual (x) with a mutated version of the virus (with a mutation that has taken place in the infecting individual), thus converting the susceptible individual to an MT-infected individual (y2A). WT-infected individuals either recover with rate a and become immune to future WT infection (z1) or die at rate d. Susceptible individuals (x) and individuals recovered from WT (z1) can become vaccinated individuals (w1). The parameter c denotes the number of individuals vaccinated per day. Hence, the rates of vaccination of x, z1 and z2 are respectively cx/(x + z1 + z2), cz1/(x + z1 + z2) and cz2/(x + z1 + z2). For simplicity, we assume single-dose vaccination. For a double-dose vaccine, our model would describe the application of the second dose ignoring partial immunity caused by the first dose. The extension of our model to a full two-dose vaccination protocol is straightforward. Although several countries display a logistic-shaped vaccine distribution curve, we show that the above linear assumption does not significantly affect the probability of emergence of vaccine resistance during the initial phase of the vaccination campaign (Supplementary Fig. 1 and Extended Data Fig. 1).

At rate β2, the MT strain infects susceptible individuals (x), WT-recovered individuals (z1) and vaccinated individuals who are not immune to MT (w1). MT-infected individuals either recover with rate a and become immune to future MT and WT infection (z2) or die at same death rate d as with the WT strain. We assume no difference in lethality between the two strains. While we consider death due to infection, the focus of this paper is not to analyse the number of deaths or public health metrics such as ICU usage or available respirators. We assume one-way cross-immunity induced by the viral strains: the MT strain can infect individuals who have recovered from WT or who have been vaccinated against WT, but the WT strain cannot infect individuals who have recovered from MT. This assumption is reasonable because MT evolves in the presence of WT, but not vice versa. We note that our MT strain escapes both the immunity induced by natural infection with WT and the immunity induced by vaccination against WT. We assume that the partial immunity to the vaccine-resistant variant induced by infection with WT is equal to that induced by vaccination. A recent study suggests that individuals who are both recovered and vaccinated benefit from higher immunity than only vaccinated individuals59. In Supplementary Figs. 2 and 3, we study this effect.

We need to distinguish between MT-infected individuals who are and are not vaccinated: y2B and y2A, respectively. Upon recovery, the former will not be vaccinated (again), while the latter will be vaccinated.

We also study partial immunity to the MT strain, which can be acquired by recovery from WT infection or by vaccination. For partial immunity, the corresponding infection rates are multiplied by a parameter q, which is between 0 and 1. If q = 1, then WT infection or vaccination confers no immunity to MT at all; MT escapes completely. For 0 < q < 1, MT is a partial escape mutant. For q = 0, MT does not escape at all.

Social distancing measures are implemented by multiplying the infectivity coefficients of each strain by a social activity parameter s, which ranges in [0, 1]. Unconstrained social interaction means s = 1, while s = 0 would be complete lockdown. The population tolerates a certain number of new infections, L, per day. Each day, if the number of new infections exceeds L, then s is decreased by a random, uniformly distributed number between 0 and s0. If the number of new infections is less than L, then s is increased by a random, uniformly distributed number between 0 and s0. In any case, s cannot decrease below 0.05 or increase above 1. In our simulations, we adjust the parameter s every day. We then obtain a near-constant number of cases per day. In Supplementary Fig. 4 and Extended Data Fig. 2, we explore less frequent adjustments of the parameter (such as every week) and conclude that our results are robust. Our social activity parameter s can be interpreted to include other factors that could affect transmissibility, such as seasonality. In Supplementary Fig. 5 and Extended Data Fig. 2, we explore the effect of seasonality.

As an example, the rate of infection of the recovered-from-WT individuals z1 by the MT-strain-infected individuals y2 is multiplied both by the social distancing coefficient s and the partial immunity coefficient q—hence, this rate is given by qβ2sw1y2.

All model parameters are summarized in Table 1.

Table 1 Summary of the model’s parameters and their biologically significant ranges
Full size table

A Gillespie algorithm is commonly used to simulate stochastic systems with high variation in waiting times between consecutive events60,61,62,63. In our model, the population is represented as a vector of length eight, corresponding to the eight categories. The rates of all possible events (infection, recovery, death, mutation and vaccination) are calculated. The time of the next event in the model is drawn from an exponential distribution with a parameter dependent on the sum of all event rates, and an event is chosen with a probability proportional to its rate. The population is updated according to the event that occurred. The simulation is stopped when there are no more infected individuals in the population.

To achieve feasible computation time and resources, we simulated populations of sizes up to N = 106. The results of those simulations can be scaled to larger population sizes by considering a population of, for example, N = 107 as m = 10 ‘batches’ of 106 individuals, and computing the results for N = 107 as 1 − (1 − p)m, where p is the proportion of runs where the MT strain took over. Extended Data Fig. 3 shows the strong agreement between the simulated results and the results scaled from simulations with smaller population sizes.

For all our simulations, we have endeavoured to use real-world data for all model parameters. In particular, infection and vaccination data have been obtained from the database Our World in Data1 (OWID) and downloaded on 29 November 2021.

In our simulation, since the number of new infections each day is constant, the number of susceptible individuals decreases linearly with slope −L/a. Vaccination of both susceptible and recovered individuals proceeds at rate c. The social activity parameter, s, increases as more and more individuals become immunized either by infection or by vaccination. The WT reproductive ratio, RWT, is maintained at 1 as long as MT has not appeared. The MT reproductive ratio, RMT, increases with the social activity parameter s until the MT strain takes over. After MT takeover, RMT is buffered at 1 by the dynamic social distancing (Extended Data Fig. 4 and Methods).

We performed 1,000 runs of the stochastic simulation for each combination of parameters reflecting realistic values of the two model parameters determined by governmental policy: L and c. Each square of the colour maps shown in Fig. 3 reflects the average value of these 1,000 runs, which were performed for a population of N = 106 and then scaled to N = 107 and N = 108. At each combination of L and c, the colour maps denote the predicted probability of an MT takeover. We perform computations using q = 1 and q = 0.4 for complete and partial immune evasion by the mutant.

Fig. 3: Probability of emergence of resistance.
figure 3

a–d, For each square of the colour maps, the proportion of runs (out of 1,000 runs) where the number of individuals infected with the MT strain exceeded the number of individuals infected with the WT strain is recorded. All simulations are run for a population size of N = 106 and then scaled to obtain the results shown for N = 107. The results for b and d were scaled according to 1 − (1 − p)10, where p is the proportion of runs where the MT strain took over. We observe a triangular shape of (L, c) parameter sets for which the MT strain takes over, indicating that high vaccination rates can be safely associated with more lenient social distancing measures. However, very slow vaccination cannot be compensated by any strength of social distancing. Partial immunity to the MT strain (c and d) does not affect the shape of the parameter space where we observe MT takeover but does reduce its probability. Parameters: a = 0.25; d = 0.01; μ = 10−6; s0 = 0.1; β1 = β2 = 7.5 × 10−7.

Full size image

Allowing a large amount of infection cases and slow vaccination results in almost certain takeover of the MT strain. In contrast, very fast vaccination coupled with a low number of tolerated new infections per day can prevent the emergence of MT. Partial immune evasion (q = 0.4) of the mutant slightly reduces the probability of its takeover. Note that the shape of the parameter space where we observe takeover is similar for q = 1 and q = 0.4. Although estimating COVID-19 mortality is not the focus of this paper, we have also recorded the number of deaths in the first 365 days of the simulation (Supplementary Fig. 6).

Results

Reproductive ratio of the mutant and probability of takeover

In Fig. 4, we show detailed data from six countries together with the estimated reproductive ratio, RMT, of a vaccine-resistant mutant and the probability of generating a wave of resistant virus. Data for the number of susceptible individuals x(t), vaccinated individuals w(t), recovered individuals z(t) and newly infected individuals L(t), as well as an estimate of RWT, can be obtained from OWID1. The reproductive ratio RMT of the escape mutant can be calculated according to:

$$R_{{\mathrm{MT}}}\left( t \right) = R_{{\mathrm{WT}}}\left( t \right)\left[ {x\left( t \right) + qw\left( t \right) + qz\left( t \right)} \right]/x(t)$$
(1)
Fig. 4: Infection and vaccination data, reproductive ratios and probability of resistance for Brazil, France, Germany, Israel, the United Kingdom and the United States.
figure 4

The total number of new cases per day and the numbers of susceptible, recovered and vaccinated individuals were downloaded from the OWID database. We used the OWID estimate of RWT to calculate the potential RMT for a full escape mutant, q = 1, and a partial escape mutant, q = 0.4 (third column). We used equation (2) to estimate the probability that an escape mutant would have emerged by time t assuming μ = 10−7 (fourth column).

Full size image

The probability of not producing an escape mutant in a given day is (1 − μ)L(t). The probability of not producing a surviving escape mutant is [1 − ρ(t)μ]L(t), where ρ(t) is the survival probability of a mutant generated on that day. If RMT(t) < 1, then ρ(t) = 0. If RMT(t) > 1, we assume that ρ(t) = 1 − 1/RMT(t). The probability that no surviving mutant is generated between time 0 and time t is given by

$$P(t) = \mathop {\prod }\limits_{\tau = 0}^t [1 - \mu \rho (\tau )]^{L(\tau )}$$
(2)

In Fig. 4, we show the reproductive ratio of the mutant RMT(t) and the probability P(t) of generating a surviving escape mutant as functions of time. Prior to vaccination, the reproductive ratio of a potential escape mutant tracks closely that of WT. As people become vaccinated in large numbers, RMT starts to increase significantly above RWT. Nevertheless, it is possible to keep RMT below one by maintaining some measures of social distancing (as was the case for Israel and the United Kingdom). Overall, the probability that Israel generated a vaccine escape mutant (before December 2021) is on the order of 1% (assuming μ = 10−7). For the same mutation rate, the corresponding probability for the United States is 75%. The United States has a much larger total population size but also allowed many more infections per million people. The corresponding probabilities for Brazil, France, Germany and the United Kingdom are 26%, 19%, 15% and 36% (Table 2).

Table 2 Calculated probability of emergence of vaccine resistance using real-world data from six countries: Brazil, France, Germany, Israel, the United Kingdom and the United States
Full size table

Estimating the mutation probability, µ

We suggest a method to estimate an upper bound of the mutation rate μ from WT to MT on the basis of the observation that despite a large number of infections since the beginning of the pandemic and including recent vaccination campaigns, no immune-evasive mutant has yet taken over. Our method for calculating an upper bound of the mutation rate is potentially applicable for estimating any mutation rate between two phenotypes in an evolving population. The upper bound is computed at any given time point and can be updated and become tighter if an evasive strain still does not appear in the future.

Let us assume that the real value of the mutation probability equals μ*. For each country, we have an estimate of the reproductive ratio of the MT strain and the number of new infection cases for each day (Fig. 4) from the beginning of the pandemic until 29 November 2021. Hence, we can calculate the probability that the MT strain would have emerged by 29 November 2021 assuming a mutation rate μ*. If this probability is higher than 0.5, then the probability that the MT strain would have been observed on 29 November 2021 is higher than not, given that the mutation rate equals μ*. Since as of 29 November 2021, an MT strain has not been observed, our estimate of the mutation rate must be lower than μ*. We define the upper bound of the mutation rate on a given day as the value μ for which the probability that the MT strain would have taken over by that day is 0.5.

Hence, for each day, we compute the probability that the MT strain would have taken over by that day given a mutation rate using equation (2). We assume q = 1, which means that the MT strain is fully immune evasive. The resulting function for the probability of MT takeover (for a given time point) versus mutation rate has a sigmoidal shape, with its midpoint corresponding to the mutation rate for which it is equally probable that the MT strain would have taken over or not (that is, our definition for the upper bound of the mutation rate). In Fig. 5a, we show the probability of emergence of the MT strain on 30 July 2020 given data from the six considered countries. The upper bound estimate for the United States is the x-axis value for the point indicated by the red arrow—that is, the midpoint of the sigmoidal function. The probability of emergence of the MT strain by 29 November 2021 for a given mutation rate is higher than it was on 30 July 2020, because many infections have occurred since then. The upper bound estimate for the United States has thus decreased—that is, shifted to the left on the x axis (see the position of the red arrow in Fig. 5b). Therefore, the estimated upper bound on the mutation rate decreases over time as long as more infections do not give rise to a MT strain (Fig. 5c).

Fig. 5: Estimating the mutation rate given that no vaccine-resistant mutant has taken over.
figure 5

a, Using equation (2), we calculate the probability that an MT strain would have taken over by 30 July 2020. To this aim, we used the numbers of new infections and immunized individuals (needed to calculate RMT at each time point) from OWID1. The probability of MT strain takeover follows a sigmoidal function, where the midpoint is reached for the value of µ at which MT strain takeover becomes more probable than not. We consider this value of µ the upper bound of the mutation rate. For the United States, the estimated upper bound of the mutation rate on 30 July 2020 would be about 10−6 (red arrow). b, Using equation (2), we calculate the probability that an MT strain would have taken over by 29 November 2021. We observe that the curves describing the probability of takeover of the MT strain along the mutation rate have shifted left. This is because since 30 July 2020, additional cases have occurred without an MT strain takeover. The upper bound of the mutation rate therefore decreases. For the United States, the upper bound would now be estimated at 2 × 10−7 (red arrow). c, The midpoint of the function (the red arrows shown in a and b) describing the probability of MT strain takeover decreases in value as more time passes without takeover of an MT strain. We use this value as an upper bound of the mutation rate for our model.

Full size image

Since the probability of MT takeover (equation (2)) is strongly dependent on the number of infections, significant decreases in the estimated values correspond to periods with high infection rates in which a mutant nonetheless did not appear. The estimate for the upper bound of the mutation rate is expected to plateau as vaccination campaigns lead to a decrease in the number of infection cases. The estimate of 10−6 will decrease further if and when large countries such as the United States advance in the vaccination campaign with no MT takeover. Using the world infection and vaccination data, we obtain μ = 10−7 as the order of magnitude for the upper bound of the rate at which immune-evasive mutants appear. But estimates based on individual countries may be more informative, since the world data reflect the average over an extremely heterogeneous population subject to very different policies.

Can we estimate a lower bound for the mutation rate? Our method could be applicable for estimating the lower mutation rate, assuming that a vaccine-resistant strain has emerged. We could then compute the value of μ given the date of emergence and assuming that the probability of emergence on that day has become higher than 0.5. Let us assume that an MT strain did take over on 29 November 2021. Then, numerically solving equation (2) by plugging in data from the United States yields μ = 2.2 × 10−7 (which is also the upper bound, assuming that the MT strain has not taken over).

A simple formula for the escape probability

The dynamic social distancing captured by the social activity parameter s(t) maintains the number of new infections per day fluctuating around a fixed value and thereby buffers RWT around 1. The number of active infections is roughly constant and is given by L/a, where a is the recovery rate (Extended Data Fig. 4). If vaccination is slow, c ≪ L, then the change in the number of susceptible individuals, x(t), and recovered individuals, z1(t), over time can be described by linear functions with slopes proportional to L (Methods and Supplementary Fig. 7a).

Alternatively, for fast vaccination, c ≫ L, the change in the number of susceptible individuals, x(t), and vaccinated individuals, w1(t), can be described by linear functions with slopes proportional to c before MT takeover, and with slopes proportional to L after MT takeover (Methods and Extended Data Fig. 4e). Neglecting vaccination of recovered individuals (which is a reasonable approximation for c ≫ L), we can write x(t) = N − Lt − ct, z(t) = Lt and w(t) = ct. The time when herd immunity against WT is reached is given by

$$T_{\mathrm{H}} = \frac{N}{{c + L}}\left( {1 - \frac{1}{{R_0}}} \right).$$
(3)

During vaccination, the reproductive ratio of MT increases as (Methods):

$$R_{{\mathrm{MT}}}\left( t \right) = \frac{N}{{N - (L + c)t}}.$$
(4)

The reproductive ratio of MT is initially 1 and increases to R0 as people recover from WT infection or are vaccinated (Extended Data Fig. 4d). Once a mutant has been generated, the probability of its survival depends on the value of RMT(t). The probability that no surviving mutant has appeared before time t, where t ≤ TH, can be calculated as (Methods):

$$P\left( t \right) = \exp \left[ { - \left( {\frac{{\mu N}}{2}} \right)\left( {\frac{L}{N}} \right)\left( {\frac{{c + L}}{N}} \right)t^2} \right].$$
(5)

The probability that no surviving mutant has appeared before herd immunity is

$$P\left( {T_{\mathrm{H}}} \right) = \exp \left[ { - \left( {\frac{{\mu N}}{2}} \right)\left( {\frac{L}{{c + L}}} \right)\left( {1 - \frac{1}{{R_0}}} \right)^2} \right].$$
(6)

Here R0 = βN/a is the basic reproductive ratio of WT. The corresponding formulas for partial immune escape mutants are given in the Methods. Equation (6) is in good agreement with the results of exact stochastic simulations (Extended Data Fig. 5). In addition, we derive P(TH) for more infectious mutants, β2 > β1 (Methods and Supplementary Fig. 8). We also explore simulation results for mutants that are less infectious than WT (Supplementary Fig. 9). We notice that P(TH) does not (strongly) depend on the parameters β, a, sthres and d (sthres is the maximal step by which the social distancing factor can be adjusted after one day). To confirm that the values of these parameters do not significantly affect the probability of emergence of a vaccine-resistant variant, we have included a sensitivity analysis in Supplementary Fig. 10.

In Table 3, we show how the probability and timing of resistance depends on the vaccination rate and the number of new infections per day. We first consider a large country of N = 108 inhabitants and a mutation probability of μ = 10−7. If 10,000 new infections occur per day and one million people are vaccinated per day, then herd immunity is reached in 66 days, and the probability of generating a vaccine-resistant mutant is about 2%. For the same vaccination rate, if 50,000 new infections are tolerated each day, then the probability of generating an escape mutant increases to 10%. If 10,000 new infections occur per day but only 100,000 people are vaccinated every day, then the probability of generating vaccine resistance increases to 18%.

Table 3 Calculated probability of vaccine resistance for a range of vaccination rates and infection rates
Full size table

As the proportion of vaccinated individuals grows, social distancing measures relax, and the probability of emergence of resistance increases. Hence, higher vaccination rates are associated with higher probabilities of resistance after 50, 100 and 200 days (Table 3). However, faster vaccination leads to earlier herd immunity. When herd immunity is reached, there are no more new infections, and the cumulative probability of resistance plateaus. We therefore observe an interesting counterintuitive effect: the probability of resistance until a fixed time t increases with the vaccination rate c, but the probability of resistance before time TH when herd immunity is achieved decreases with c (Table 3 and Extended Data Fig. 6).

We can derive estimates for the emergence of vaccine-resistant strains using current vaccination and infection rates from around the world. If the whole world (N = 8 × 109) vaccinated as fast as the United States (c = 5,000 per day per million) and had slightly lower infection rates than Germany (L = 100 per day per million), then herd immunity would be achieved in TH = 131 days; the probability that a resistant virus was generated and survived by that time would be 0.97 (for μ = 10−7) and 0.29 (for μ = 10−8). If the whole world vaccinated as fast as Brazil (c = 3,000 per day per million) and had infection rates like the United States (L = 250 per day per million), then herd immunity would be achieved in TH = 205 days; the probability that a resistant virus was generated and survived by that time would be 0.999 (for μ = 10−7) and 0.75 (for μ = 10−8). Our results underline the importance of maintaining social distancing measures while herd immunity has not been achieved and of timely distribution of vaccines around the world.

Preventing the emergence of vaccine resistance

Improved vaccine design

The probability of emergence of vaccine resistance can be reduced by increasing the number of vaccinated people per day (c) and reducing the number of allowed infections per day (L) until herd immunity is reached. However, policymakers could also affect the mutation rate µ by determining what type of vaccine is used. We have extended our basic model to consider vaccine resistance achieved when two independent mutations are present (Supplementary Figs. 11 and 12). Each mutation is neutral by itself. We find that for realistic mutation rates (that is, mutation rates below our estimated upper bound), vaccine resistance never emerges when two-gene vaccines are distributed (Extended Data Fig. 7). This extension can also be interpreted as the case where two independent mutations are needed to confer resistance to a vaccine based on a single gene. But using two mRNAs in a single vaccine could double the number of mutations needed to achieve immune escape.

Reducing vaccine hesitancy

In most developed countries, vaccine hesitancy has caused the number of vaccinated individuals to plateau. Vaccine hesitancy can also be reduced by policy decisions64. In Supplementary Fig. 13 and Extended Data Fig. 8, we extend our model to account for the proportion of the population that will not be vaccinated. We find that although high vaccine hesitancy substantially increases the probability of emergence of vaccine resistance, low vaccine hesitancy can actually have a negligible effect. For R0 = 3, the levels of vaccine hesitancy necessary to significantly increase the probability of emergence of vaccine resistance are much higher than the vaccination hesitancy rates in many of the considered countries except for Brazil and the United States65,66. However, more infectious mutants have emerged in the past few months.

To achieve herd immunity, a certain fraction of the population must become immunized to the infecting agent. Immunization can occur either by recovery from infection or by vaccination. The minimum fraction of immunized people required for herd immunity increases with the reproductive ratio R. If a certain proportion of the population will not be vaccinated, then an excess of infections will occur to achieve the proportion of immunized people required for herd immunity. This excess of infections increases the probability of emergence of vaccine resistance. For R0 = 3, the fraction of immunized people required for herd immunity is 2/3. Hence, 1/3 of the population can remain susceptible without affecting the probability of emergence of a vaccine-resistant variant. However, with more infectious variants, this tolerated proportion of non-vaccinated people is lower. For example, for R = 5, the proportion of non-vaccinated people such that the probability of vaccine emergence is unchanged is only 20%. As vaccination is expected to be extended to more age groups, the proportion of unvaccinated individuals could further decrease until vaccine hesitancy ceases to be a concern for the emergence of vaccine resistance.

In most countries, vaccine hesitancy seems to be a function of age. We can therefore estimate the expected vaccine hesitancy given the age structure of each of the six countries. In Israel, 89% of 60- to 69-year-olds are fully vaccinated, versus 75% of 20- to 29-year-olds65,66. In France, 83% of 60- to 69-year-olds are fully vaccinated, versus 76% of 25- to 49-year-olds. In some countries, vaccination of the younger population has not reached a plateau, such as in Bulgaria, Peru and Romania65,66. In these countries, we expect that many people are still being vaccinated and hence the total amount of vaccinated individuals will increase.

Using boosters to counteract waning of immunity

Waning of immunity has become a concern. We have extended our model to consider waning of immunity beginning 180 days after vaccination or recovery (Supplementary Figs. 14 and 15). When no booster vaccination is administered, the probability of emergence of vaccine resistance increases substantially, especially for high vaccination rates. However, a booster vaccination campaign conducted after 180 days can reduce the probability of emergence of vaccine resistance back to basic model levels (Extended Data Fig. 9).

Discussion

We have studied the evolution of resistance to COVID-19 vaccination in the presence of dynamic social distancing. We use real-world data to simulate the spread of the SARS-CoV-2 virus. We have performed stochastic simulations and obtained analytical results. In particular, we have derived a simple, intuitive formula for the probability of emergence of a vaccine-resistant strain over time (equations (5) and (6)).

Our basic model makes a series of simplifying assumptions: (1) no seasonality of the infection patterns, (2) vaccination of the whole population, (3) no waning of immunity, (4) linear distribution of vaccine doses and (5) rapid social response to rising infection numbers. We have studied model extensions that remove these simplifications (Supplementary Figs. 1–5, 8, 9 and 11–15 and Extended Data Figs. 1, 2 and 7–9). We have assumed a stochastic model because the appearance of a vaccine-resistant strain, and in particular its non-extinction due to random drift, is by nature stochastic.

Some of the simplifying assumptions made in our approach should be revisited in future work. We have described the transition from a sensitive variant to a resistant (or partially resistant) mutant as a single probabilistic step. It would be desirable to study viral evolution of vaccine resistance as a gradual process including multiple intermediate variants, some of which could be neutral, while others modify infectivity or enable partial escape. Using an SIR-like model, we did not consider spatial or network effects of viral transmission or vaccination. We did not distinguish between symptomatic and asymptomatic individuals. Symptomatic infection might give rise to different infectivity and recovery rates because of self-isolation.

The probability of takeover of an immune-evasive strain is mostly dependent on the number of total infection cases that occur during the pandemic. Social distancing measures, such as lockdowns, can delay or even prevent the emergence of the MT strain. Each natural infection is an opportunity for the MT strain to appear and possibly take over. Hence, the main policy goal should be to maximize the proportion of the population that will be immunized to the virus through vaccination as opposed to natural infection.

In terms of policy implications, our results support the maintenance of social distancing (or contact reducing) measures, such as lockdowns, restrictions on building capacity and guidance on homeworking, until the daily number of infections decreases substantially. Allowing a large number of infections can be counterbalanced only by very high vaccination rates, which ensure that herd immunity is reached before the MT strain can appear and take over. Furthermore, our results underline the importance of a worldwide effort to quickly vaccinate as many individuals as possible, especially in highly populated countries with low access to vaccines. Slow or no vaccination in those areas results in a large number of total cases and hence the emergence of an MT strain, which could then spread over the whole world.

Methods

Data accession

Data for vaccination rates, infection rates and mortality rates were downloaded from https://ourworldindata.org/explorers/coronavirus-data-explorer using the ‘Download’ button under the chart and selecting the option ‘Full Data (CSV)’. Subsequent analysis was performed with Python v.367; our code is available at https://github.com/gabriela3001/covid_resistance_2021.

Vaccination data on specific age groups were downloaded from https://ourworldindata.org/covid-vaccinations under the tab ‘Vaccination by age’.

Derivation of mathematical results

All of the stochastic simulations presented in Fig. 3 and Extended Data Fig. 4 were run with the full model presented in Fig. 2. In the following derivations, however, we make certain approximations to obtain analytical results. Among others, we neglect death, and in some cases we neglect vaccination of recovered individuals.

No vaccination

First, we consider the case without vaccination. We denote by x the number of susceptible individuals, by y the number of individuals infected with WT and by z the number of individuals recovered from WT. The infection rate is β, the recovery rate a, the mutation rate μ and the population size N. The social activity parameter s(t) captures the extent of imposed social distancing that varies over time. For simplicity, we neglect the number of individuals who die; hence, N is assumed to be constant.

Deterministic WT infection dynamics are given by the following system of differential equations:

$$\begin{array}{l}\dot x = - \beta sxy\\ \dot y = \beta sxy - ay\\ \dot z = ay\end{array}$$
(7)

Initially, all of the population is susceptible to the WT strain, and no individuals are infected with or recovered from the WT strain. We therefore have x(0) = N, y(0) = 0 and z(0) = 0. Social activity, s(t), is adjusted such that y(t) = L/a is constant (Extended Data Fig. 4c). L is the number of new infections per day.

Without social distancing, s = 1, the basic reproductive ratio of WT is given by R0 = βN/a. If R0 > 1, the number of infected individuals grows initially. With social distancing, s < 1, the reproductive ratio is RWT = βNs/a. Since the social distancing measures maintain y(t) = L/a at a constant value, we have RWT = 1 and βs(t)x(t) = a (Supplementary Fig. 7). The parameter s can vary between 0 and 1. Note that the maintenance of the number of infection cases at a constant value, which follows directly from social distancing measures maintaining the viral reproductive ratio at 1, allows us to obtain an analytical expression for the number of immunized individuals over time. This expression will then be instrumental in deriving the probability of emergence of a vaccine-resistant mutant over time, and finally the probability of emergence of a vaccine-resistant mutant before herd immunity is reached.

Although RWT and RMT are initially equal, they do not remain equal at any later time point. This is because the reproductive ratios of the WT strain and MT strain are dependent on the number of individuals that can be infected by WT and the number of individuals that can be infected by MT. Initially, both strains can infect the whole population. As the simulation progresses, the WT strain can infect fewer individuals due to the recovery of WT-infected individuals and due to vaccination. However, the MT strain can still potentially infect every individual in the population, since WT-recovered individuals and vaccinated individuals are susceptible to MT.

Each day, L individuals become infected, and L individuals recover. Because of dynamic social distancing, the following equation is equivalent to equation (7):

$$\begin{array}{l}\dot x = - L\\ \dot y = 0\\ \dot z = L\end{array}$$
(8)

The solution to this system of differential equations is

$$\begin{array}{l}x\left( t \right) = N - Lt\\ z\left( t \right) = Lt\end{array}$$
(9)

Hence, the number of susceptible individuals decreases linearly with slope L, while the number of recovered individuals increases linearly with slope L (see Supplementary Fig. 7 for agreement with the stochastic simulation).

When x(t) has declined such that RWT < 1 and s = 1, there are not enough susceptible individuals to sustain the infection. Herd immunity is achieved when x(t) < a/β. The time TH until herd immunity is given by β(N − Lt) = a. We obtain

$$T_{\mathrm{H}} = \frac{N}{L}\left( {1 - \frac{1}{{R_0}}} \right)$$
(10)

Rate of generating mutants in the absence of vaccination

Each day, L new individuals become infected. Each of these infections has a probability μ of being a vaccine-resistant mutant. Hence, the rate of producing a mutant is Lμ per day. Let P(t) denote the probability that no mutant has been produced until time t. We have \(\dot P(t) = - L\mu P(t)\), which leads to P(t) = e−Lμt.

The MT strain can be generated only during infection. Hence, if the MT strain has not been generated before the time when there are no more WT infections—that is, approximately when herd immunity is reached—it will never be generated. We neglect here the time of exponential decrease in the number of WT infections between time TH (when herd immunity is reached) and the time when the number of WT infections has reached zero. The probability that no mutant will appear before time TH is P(TH) = \({\rm{e}}^{-L{\mu}T_{\rm{H}}}\). Inserting from equation (4), we obtain

$$P(T_{\mathrm{H}}) = {{{\mathrm{exp}}}}\left[ { - N\mu \left( {1 - \frac{1}{{R_0}}} \right)} \right]$$
(11)

Rate of generating surviving mutants in the absence of vaccination

To calculate the probability that MT will be generated and survive, we need to multiply the rate of generation of MT with the probability that it will not become extinct by random drift. If ρ(t) is the survival probability of MT, then the rate of producing a surviving mutant is Lμρ(t) per day. We approximate ρ(t) = 1 − 1/RMT(t), where RMT(t) is the reproductive ratio of the mutant at time t.

We have

$$R_{{\mathrm{MT}}}\left( t \right) = \beta s\left( t \right)N/a$$
(12)

Since s(t) = a/βx(t) and using equation (9), we obtain

$$R_{{\mathrm{MT}}}\left( t \right) = \frac{N}{{N - Lt}}$$
(13)

We therefore have ρ(t) = Lt/N.

Let P(t) denote the probability that no surviving mutant has been produced before time t. We have \(\dot P\left( t \right) = - L\mu \rho \left( t \right)P\left( t \right) = - L^2\mu tP(t)/N\). We solve this differential equation to obtain P(t) = exp(−μL2t2/2N). The probability that no surviving mutant has been produced before herd immunity, which is reached at time TH, is given by

$$P\left( {T_{\mathrm{H}}} \right) = {{{\mathrm{exp}}}}\left[ { - \frac{{\mu N}}{2}\left( {1 - \frac{1}{{R_0}}} \right)^2} \right]$$
(14)

With vaccination

Let us now add vaccination. Denote by w the number of vaccinated people. If both recovered and susceptible individuals are vaccinated at a total rate of c per day, then deterministic infection and vaccination dynamics are given by

$$\begin{array}{l}\dot x = - \beta sxy - \frac{{cx}}{{x + z}}\\ \dot y = \beta sxy - ay\\ \dot z = ay - \frac{{cz}}{{x + z}}\\ \dot w = c\end{array}$$
(15)

The initial condition is x(0) = N, y(0) = 0, z(0) = 0, w(0) = 0, s(0) = 1 and R0 = βN/a. As before, we adjust s(t) such that y(t) = L/a is constant (Extended Data Fig. 4).

Each day, L susceptible individuals become infected, and cx/(x + z) susceptible individuals become vaccinated. Also, L infected individuals recover, and cx/(x + z) of recovered individuals become vaccinated. We have:

$$\begin{array}{l}\dot x = - L - \frac{{cx}}{{x + z}}\\ \dot y = 0\\ \dot z = L - \frac{{cz}}{{x + z}}\\ \dot w = c\end{array}$$
(16)

For simplicity, let us assume that we vaccinate only susceptible people. This assumption is a reasonable approximation if c ≫ L. In this case, we can write

$$\begin{array}{l}\dot x = - L - c\\ \dot y = 0\\ \dot z = L\\ \dot w = c\end{array}$$
(17)

The solution to this system of differential equations is

$$\begin{array}{l}x\left( t \right) = N - Lt - ct\\ z\left( t \right) = Lt\\ w(t) = ct\end{array}$$
(18)

Hence, the number of susceptible individuals decreases linearly with slope L + c, the number of recovered individuals increases with slope L and the number of vaccinated individuals increases with slope c.

The time TH until herd immunity is given by

$$T_{\mathrm{H}} = \frac{N}{{c + L}}(1 - 1/R_0)$$
(19)

Rate of generating mutants during vaccination

The rate of producing a mutant is Lμ per day. Let P(t) denote the probability that no mutant has been produced before time t. We have \(\mathop {{P(t)}}\limits^. = - L\mu P(t)\), which gives P(t) = exp(−Lμt).

The MT strain can be generated only during infection. Hence, if the MT strain has not been generated before the time when there are no more WT infections—that is, when herd immunity is reached—it will never be generated. Again, we neglect here the time of exponential decrease in the number of WT infections between the time TH when herd immunity is reached and the time when the number of WT infections reaches 0. Hence, the probability that no mutant will appear is P(TH) = exp(−LμTH). Using equation (19), the probability that no mutant has appeared before herd immunity is

$$P\left( {T_{\mathrm{H}}} \right) = {{{\mathrm{exp}}}}\left[ { - N\mu \left( {\frac{L}{{c + L}}} \right)\left( {1 - \frac{1}{{R_0}}} \right)} \right]$$
(20)

Rate of generating surviving mutants during vaccination

To calculate the probability that surviving mutants are generated, we again consider the survival probability ρ(t) = 1 − 1/RMT(t), where RMT(t) is the reproductive ratio of the mutant at time t. The rate of producing a surviving mutant is Lμρ(t) per day. We have

$$R_{{\mathrm{MT}}}\left( t \right) = \frac{{\beta s\left( t \right)N}}{a}$$
(21)

As explained above, s(t) = a/βx(t). Using equation (18), we obtain

$$R_{{\mathrm{MT}}}\left( t \right) = \frac{N}{{N - (L + c)t}}$$
(22)

And therefore, ρ(t) = (L + c)t/N.

Let P(t) denote the probability that no surviving mutant has been produced before time t. We have \(\dot P\left( t \right) = - L\mu \rho \left( t \right)P(t) = - L\mu (c + L)tP(t)/N\). Let v = c/N and l = L/N. We solve this differential equation to obtain

$$P\left( t \right) = {{{\mathrm{exp}}}}\left[ { - \frac{{\mu N}}{2}l(v + l)t^2} \right]$$
(23)

The probability that no surviving mutant has been produced before herd immunity, at time TH, is

$$P\left( {T_{\mathrm{H}}} \right) = {{{\mathrm{exp}}}}\left[ { - \frac{{\mu N}}{2}\left( {\frac{l}{{v + l}}} \right)\left( {1 - \frac{1}{{R_0}}} \right)^2} \right]$$
(24)

Rate of generating surviving mutants with partial immune escape during vaccination

We study the case where the infectivity of the mutant is reduced by a factor q with range [0,1] when infecting recovered or vaccinated people. For q = 1, we obtain full escape, while q = 0 means that the mutant does not escape at all.

A similar derivation to the one above leads to the following result. The probability that no surviving mutant with partial escape q has appeared before herd immunity is given by

$$\begin{array}{rcl}P\left( {T_{\mathrm{H}}} \right) = {{{\mathrm{exp}}}}\left[ { - \frac{{\mu N}}{2}\left( {\frac{l}{{v + l}}} \right)A} \right]\,{{{\mathrm{with}}}}\,A = \frac{{2q}}{{1 - q}}\\ \left[ { - \frac{{R_0 - 1}}{{R_0}} + \frac{1}{{1 - q}}\log \frac{{R_0}}{{1 + q(R_0 - 1)}}} \right]\end{array}$$
(25)

For q → 1, we obtain A = (1 − (1/R0))2, leading to equation (23) above.

Relationship between the product formula and the exponential formula

Each day, L new WT infections occur. Each new infection has a probability of μ of being the MT strain. The survival probability of the mutant is approximately 1 − 1/RMT(t), where RMT(t) is the basic reproductive ratio of MT appearing at time t.

Hence, the probability that none of the L new WT infections in a day will generate a surviving mutant is {1 − μ[1 − 1/RMT(t)]}L. We can then write the probability P that no surviving mutant will be produced between time t = 0 and the time TH when herd immunity is reached as the product

$$P = \mathop {\prod }\limits_{\tau = 0}^{T_{\mathrm{H}}} \left[ {1 - \mu \left( {1 - \frac{1}{{R_{{\mathrm{MT}}}(\tau )}}} \right)} \right]^L$$
(26)

We have TH = [N/(c + L)](1 − 1/R0) and RMT(t) = N/[N − (c + L)t]. Since ρ(t) = 1 − 1/RMT(t) = (c + L)t/N, we can write

$$P = \mathop {\prod }\limits_{\tau = 0}^{T_{\mathrm{H}}} \left[ {1 - \frac{{\mu \left( {c + L} \right)\tau }}{N}} \right]^L$$

Let us use the abbreviation u = μ(c + L)/N. Then

$$\begin{array}{*{20}{l}} P \hfill & = \hfill & {\mathop {\prod}\limits_{\tau = 0}^{T_{\mathrm{H}}} {(1 - u\tau )} ^L} \hfill \\ {} \hfill & = \hfill & {{{{\mathrm{exp}}}}\left[ {{\mathrm{log}}\mathop {\prod}\limits_{\tau = 0}^{T_{\mathrm{H}}} {(1 - u\tau )} ^L} \right]} \hfill \\ {} \hfill & = \hfill & {{{{\mathrm{exp}}}}\left[ {L{\mathrm{log}}\mathop {\prod}\limits_{\tau = 0}^{T_{\mathrm{H}}} {(1 - u\tau )} } \right]} \hfill \\ {} \hfill & = \hfill & {{{{\mathrm{exp}}}}\left[ {L\mathop {\sum}\limits_{\tau = 0}^{T_{\mathrm{H}}} {{{{\mathrm{log}}}}} (1 - u\tau )} \right]} \hfill \end{array}$$
(27)

Note that equation (26) is exactly equivalent to equation (23). Assuming uTH ≪ 1, which is the same as μ(1 − 1/R0) ≪ 1, we obtain

$$\begin{array}{*{20}{l}} P \hfill & = \hfill & {{{{\mathrm{exp}}}}\left( { - uL\mathop {\sum}\limits_{\tau = 0}^{T_{\mathrm{H}}} \tau } \right)} \hfill \\ {} \hfill & = \hfill & {\exp \left[ { - \frac{{uLT_{\mathrm{H}}\left( {T_{\mathrm{H}} + 1} \right)}}{2}} \right]} \hfill \end{array}$$

Assuming TH ≫ 1, which is N(1 − 1/R0) ≫ c + L, we obtain

$$\begin{array}{l}P = \exp \left( { - \frac{{uLT_{\mathrm{H}}^2}}{2}} \right)\\ = \exp \left[ { - \frac{{(\mu (c + L)/N)LT_{\mathrm{H}}^2}}{2}} \right]\end{array}$$

Finally, inserting TH = [N/(c + L)](1 − 1/R0), we get

$$P\left( {T_{\mathrm{H}}} \right) = {{{\mathrm{exp}}}}\left[ { - \frac{{\mu N}}{2}\left( {\frac{l}{{v + l}}} \right)\left( {1 - \frac{1}{{R_0}}} \right)^2} \right]$$
(28)

which is equivalent to equation (24) above.

Dynamics after the appearance of the MT strain

No vaccination

After the MT strain has taken over, social distancing measures will continue maintaining the number of daily infections at L, which implies that y1 + y2 = L/a (Supplementary Fig. 7). In practice, the WT strain rapidly goes extinct upon the emergence of the MT strain, so we can consider y2 = L/a. The MT strain can infect susceptible individuals, x, and recovered individuals, z1. The MT strain infects those individuals with probabilities proportional to their frequencies at the time t* of MT takeover. Hence, for times t > t*, we have:

$$\begin{array}{l}x\left( t \right) = x\left( {t^ \ast } \right) - \frac{{x\left( {t^ \ast } \right)}}{{z_1\left( {t^ \ast } \right) + x\left( {t^ \ast } \right)}}L\left( {t^ \ast - t} \right)\\ z_1\left( t \right) = z_1\left( {t^ \ast } \right) - \frac{{z_1\left( {t^ \ast } \right)}}{{z_1\left( {t^ \ast } \right) + x\left( {t^ \ast } \right)}}L\left( {t^ \ast - t} \right)\end{array}$$
(29)

After MT takeover, the social distancing measures need to be readjusted to the MT strain. Since more individuals are susceptible to it, s(t) has to decrease (Supplementary Fig. 7f):

$$s\left( t \right) = \frac{{aN}}{{\beta \left[ {x\left( t \right) + qz_1\left( t \right)} \right]}}$$
(30)

which implies that RMT = 1.

With vaccination

As for the case without vaccination, if the MT strain survives, it will quickly replace the WT strain such that y2 = L/a (Extended Data Fig. 4c). The number of susceptible individuals x(t*) at the time of MT takeover can be neglected for large enough vaccination rates. The number of vaccinated individuals susceptible to the MT strain, w1, will hence decrease linearly with the number of tolerated cases per day, L, and the number of vaccinated individuals recovered from the MT strain, w2, will increase complementarily linearly with L. If the mutant takes over at time t*, we have for all times t > t*:

$$\begin{array}{l}w_1\left( t \right) = w_1\left( {t^ \ast } \right) - L(t^ \ast - t)\\ w_2\left( t \right) = L(t^ \ast - t)\end{array}$$
(31)

The social activity parameter s needs readjustment to consider the additional groups of individuals that are now susceptible to the infecting strain. We have

$$s\left( t \right) = \frac{a}{\beta }\times\frac{{x\left( t \right) + q[z_1(t) + w_1(t)]}}{{x\left( t \right) + q[z_1(t) + w_1(t)] - w_2\left( t \right)}}$$
(32)

which ensures that RMT = 1. Here the parameter q in [0, 1] denotes the extent of escape.

Estimating the evolutionary potential of the virus

If μ is the mutation probability as described above and L(t) is the time series giving the number of new infections on day t, then the probability that no mutant has been produced between time 0 and time TH is given by

$$P\left( {T_{\mathrm{H}}} \right) = \mathop {\prod}\limits_{\tau = 0}^{T_{\mathrm{H}}} {(1 - \mu )^{L(\tau )}}$$
(33)

This probability will overestimate the evolutionary potential of the virus to escape from vaccination because many mutants do not survive the initial random drift. The probability that no surviving mutant has been produced between time 0 and time TH can be written as

$$P\left( {T_{\mathrm{H}}} \right) = \mathop {\prod}\limits_{\tau = 0}^{T_{\mathrm{H}}} {[1 - \mu \rho (\tau )]^{L(\tau )}}$$
(34)

Here ρ(t) is the survival probability of an escape mutant produced at time t. This probability depends on the basic reproductive ratio of the mutant on the day it is being produced (and the next few days until random drift is negligible). Approximately, we can write

$$\rho \left( t \right) = \min \left\{ {0,1 - \frac{1}{{R_{\mathrm{MT}}(t)}}} \right\}$$
(35)

For the potential of the virus to generate mutants (irrespective of whether they survive), what matters most is the total number of infections, ΣτL(τ). But for the potential of the virus to generate surviving mutants, one must also consider the time periods when social distancing is relaxed such that RMT is above 1.

Analytic approximation for more infectious, vaccine escape mutants

No vaccination

Now we calculate the probability that mutants are being generated that do become extinct by random drift. We denote f the relative infectiousness of the MT versus the WT strain. Hence, for more infectious mutants, we have f > 1. The rate of producing a surviving mutant is Lμρ(t) per day. Here ρ(t) is the survival probability given by ρ(t) = 1 − 1/RMT(t). The basic reproductive ratio of the mutant at time t is RMT(t) = fβs(t)N/a. Since βs(t)N/a = 1/x(t), we have RMT(t) = fN/(N − Lt), and therefore:

$$\rho \left( t \right) = 1 - \frac{1}{{R_{\mathrm{MT}}\left( t \right)}} = \frac{{N( {f - 1} ) + Lt}}{{Nf}}$$
(36)

Let P(t) denote the probability that no surviving mutant has been produced before time t. We have \(\dot P\left( t \right) = - L\mu \rho \left( t \right)P(t)\). Thus, \(\dot P\left( t \right) = \left( {\kappa + \lambda t} \right)P(t)\), with the solution \(P\left( t \right) = {{{\mathrm{exp}}}}\left( {\kappa t + \frac{\lambda }{2}t^2} \right)\), which already leads to P(0)=1, as desired. In our original notation, the solution becomes:

$$P\left( t \right) = {{{\mathrm{exp}}}}\left[ { - L\mu \frac{{N( {f - 1} )}}{{Nf}}t - L\mu \frac{{Lt}}{{2Nf}}t^2} \right]$$
(37)

With vaccination

The rate of producing a surviving mutant is Lμρ(t) per day. Here ρ(t) is the survival probability given by ρ(t) = 1 − 1/RMT(t). The basic reproductive ratio of the mutant at time t is RMT(t) = fβs(t)N/a. Since βs(t)N/a = 1/x(t), we have RMT(t) = fN/[N − (c + L)t], and:

$$\rho (t) = 1 - \frac{1}{{R_{\mathrm{MT}}\left( t \right)}} = \frac{{N( {f - 1} ) + (c + L)t}}{{Nf}}$$
(38)

Let P(t) denote the probability that no surviving mutant has been produced before time t. We have \(\dot P\left( t \right) = - L\mu \rho \left( t \right)P(t)\). Thus:

$$\dot P( t ) = - L\mu \frac{{N( {f - 1} ) + ( {c + L} )t}}{{Nf}}P(t)$$
(39)

This solution of this differential equation is given by:

$$P\left( t \right) = {{{\mathrm{exp}}}}\left( { - L\mu \frac{{f - 1}}{f}t - L\mu \frac{{c + L}}{{2Nf}}t^2} \right)$$
(40)

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.