Main

Accelerating a quantum particle on an ideal periodic lattice potential leads to oscillatory motion instead of a net drift. This counter-intuitive phenomenon, known as Bloch oscillations (BOs), has been observed in various contexts ranging from solid-state experiments1 to synthetic lattice systems involving matter waves2 or light3,4,5. Besides enabling direct observations of BOs (and other phenomena6,7,8), the efficient control and agility characteristic of synthetic lattices offer a route for judiciously exploring how effects such as non-linearities, dissipation and Bloch band properties influence the oscillation dynamics. Quite generically, the existence of long-lived BOs (correlated to a persistent scan of the full Brillouin zone) is endangered by dissipation9 and instabilities associated with non-linearities3,10,11,12. Although methods have been proposed to prevent such instabilities13,14, the observation of long-lived BOs is still lacking in the realm of non-linear waves. Furthermore, the impact of dissipative effects (for example, loss and gain of energy) on the BOs of non-linear waves has remained largely unexplored15. Here, we address these fundamental questions by demonstrating that long-lived BOs can exist in a driven–dissipative and non-linear environment via the formation of localized dissipative structures (solitons).

Beyond fundamental questions regarding their existence and stability, BOs constitute a practical probe for revealing the band structure of synthetic lattice systems. For instance, driving BOs on a one-dimensional lattice directly reflects the bandwidth, the Brillouin zone and the effective mass of the underlying band structure2. Moreover, BOs can be used to extract the geometry and topology of engineered topological systems, such as the quantized Zak phase of one-dimensional (1D) chiral systems16. These BO-based probes can be extended to two-dimensional (2D) engineered systems to extract the Berry curvature17,18, quantized Wilson loops19,20,21 or the winding numbers of Floquet phases18. As such, exploring the specific features of BOs in the presence of non-linearity and dissipative effects is crucial to elucidating the properties of unconventional synthetic systems where such effects play a key role.

Designing real (physical) periodic structures for photons and matter waves constitutes a natural path towards the realization of synthetic lattices and quantum simulators7,8. Interestingly, an alternative method has recently emerged by which motion is engineered along a synthetic dimension formed through coupling of the discrete degrees of freedom of a system22. First envisioned for creating photonic lattices with high dimensionality via complex networks23, and then widely exploited in ultracold gases24,25,26,27, the concept of synthetic dimensions has been extensively explored in the realm of photonics using diverse optical platforms28,29,30,31,32,33,34. In particular, pioneering experiments5,31 have shown that different frequency modes of an optical cavity can be used to represent an array of fictitious lattice sites, with motion along this lattice generated by an electro-optical modulator (EOM) inserted inside the cavity (Fig. 1a). Such a setting was recently exploited to realize artificial gauge fields for light35,36,37 and to reveal topological windings of non-Hermitian bands38. However, these experiments have so far focused on operating regimes that are linear and predominantly conservative (albeit with some dissipative effects acting as unwanted perturbations). Under such conditions, group velocity dispersion (and other experimental constraints) strongly limits the extent of the synthetic array. However, of course, the particular (fibre-optic) cavity configurations used in recent experiments31,39 can also be operated under conditions where a strong optical (Kerr-type) non-linearity introduces non-local coupling between the fictitious lattice sites28,32,34. This observation raises immediate (as yet unrealized) opportunities for systematically exploring how non-linearities and dissipative effects can influence BOs. More generally, the possibility of controllably combining synthetic lattices with non-linearities could open the door to non-linear topological physics40,41,42,43,44, with BOs offering a versatile tool for probing the systems’ properties.

Fig. 1: Concept.
figure 1

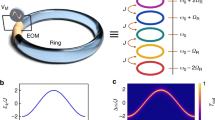
a, A schematic illustration of the experimental implementation, consisting of a coherently driven optical ring resonator with a Kerr-type non-linearity that incorporates an EOM to realize coupling between different cavity modes. The EOM engenders hopping between resonator modes separated by an integer number of the cavity FSR, thus yielding a tight-binding lattice in the synthetic (frequency) space. An EDF amplifier is also inserted into the cavity to compensate for the losses induced by the EOM. b, In the non-linear regime, a temporal CS is generated within the resonator. The soliton is associated with a broad coherent optical frequency comb, thus extending the size of the synthetic frequency lattice with numerous equally spaced sites (the shading represents the CS spectrum, from low (red) to high (blue) frequencies). The corresponding band energy and intensity profile of the CS along the Brillouin zone are illustrated in the top-right inset. c–e, A constant force F can be introduced along the synthetic frequency dimension by detuning the frequency of the intra-cavity EOM from an integer multiple of the cavity FSR, thus forcing the CS to undergo transport along the synthetic lattice; as the effective force F increases, the soliton’s transport changes from synchronization (c) to nascent oscillations (d), and finally to ideal BOs (e). Blue scale of the dots in panels c–e represents different spectral densities.

Full size image

Concurrently, the non-linear dynamics of coherently driven Kerr-type resonators have been extensively studied in the absence of an intracavity EOM (and hence without a synthetic frequency dimension)45,46,47,48,49,50,51,52,53,54,55,56. It is well established that such dissipative systems can host a number of universal non-linear phenomena45,46,47,53, among which the emergence of localized structures known as temporal cavity solitons (CSs) has attracted particular attention. First observed in an optical fibre ring resonator48, temporal CSs are fundamentally underpinned by a double-balance between linear dispersive spreading and non-linearity, as well as energy loss and gain (via an external coherent driving) of the resonator. Subsequently, CSs have been extensively studied in the context of monolithic microresonators, where they have been shown to be associated with the formation of broad and coherent optical frequency combs51,57,58. Interestingly, while CSs and resonator-based synthetic dimensions have been studied in similar platforms, there is little overlap between the two domains of research34,59. This is somewhat surprising since the intrinsic features of CSs yield all the ingredients essential to exploit the full potential of synthetic frequency dimensions, that is, a short, robust temporal structure capable of scanning the whole Brillouin zone with high resolution and a broad, coherent, equally spaced comb spectrum that allows one to substantially extend the number of modes that can be coupled in the synthetic frequency dimension—a combination of properties that is not straightforward to attain in linear or conservative systems5,31,60. It is only very recently that a theoretical study explored how dissipative CSs behave in the presence of an intra-cavity EOM implementing a synthetic frequency dimension61. However, the difficulty of including an intra-cavity EOM while maintaining low intra-cavity losses, a prerequisite for CS existence, has so far prevented experimental investigations.

Here, by leveraging a recently developed active cavity scheme55 to compensate for the losses incurred by an intra-cavity EOM, we experimentally explore the non-linear dynamics of dissipative Kerr CSs in a synthetic frequency dimension, thus bridging the gap between the realms of synthetic photonic lattices and non-linear Kerr resonators. In addition to exploring the predictions of ref. 61, we implement an effective force along the synthetic lattice and demonstrate that CSs can undergo long-lived BOs whose specific features can be substantially influenced by the presence of dissipation and non-linearity. Our results establish Kerr resonators as an ideal platform to explore Bloch band transport in open non-linear dissipative systems that are driven out of equilibrium, with potential implications for optical frequency combs and topological photonics8,22,41.

Principle and theoretical description

We begin by describing the analogy (and the limitations of the analogy) between a quantum particle on a periodic lattice and a coherently driven Kerr resonator31,48. To this end, we consider a ring resonator with an intra-cavity EOM that imparts a sinusoidal phase modulation (with amplitude JEOM) on the field circulating inside the resonator, with the modulation frequency fEOM set close to an integer multiple of the resonance frequency spacing of the cavity (the free-spectral range, FSR): fEOM = m × FSR + Δf, with \(m\in {\mathbb{N}}\) and Δf ≪ FSR (Fig. 1a). As described in ref. 29, the EOM permits an excitation in the nth cavity mode to effectively hop into nearby modes n ± m along the frequency axis, thus mimicking a tight-binding model of a quantum particle moving along a 1D lattice. Therefore, under conditions of negligible non-linearity (low intra-cavity power), weak dispersion and balance between loss and driving, this optical system can be described by a linear Schrödinger equation (with ℏ = 1) associated with the following conservative tight-binding Hamiltonian (Methods):

$$\hat{H}=-J\mathop{\sum}\limits_{n}(\left\vert n\right\rangle \left\langle n-1\right\vert +\left\vert n\right\rangle \left\langle n+1\right\vert )+(Fd)\mathop{\sum}\limits_{n}n\left\vert n\right\rangle \left\langle n\right\vert,$$
(1)
$$=-\int\left\vert \tau \right\rangle \left\langle \tau \right\vert \,\left\{2J\cos (d(\tau -Ft))\right\}\,{{{\rm{d}}}}\tau ,$$
(2)

where the states are labelled such that \(\left\vert n\pm 1\right\rangle\) correspond to the cavity modes n ± m coupled by the EOM. The first term of equation (1) describes hopping between neighbouring sites \(\left\vert n\right\rangle \to \left\vert n\pm 1\right\rangle\) of the lattice with hopping amplitude J = JEOM × FSR/2, whereas the second term describes the action of an additional constant force F = Δf/fEOM ≈ Δf/(m × FSR) along the lattice, with d = 2π × m × FSR ≡ Ωm an effective inter-site distance (m = 100 and FSR ≈ 3 MHz in the experiments described in Fig. 2). Equation (2) corresponds to the dual-space representation of the Hamiltonian: the ‘momentum’ coordinate τ belongs to the first Brillouin zone [−π/d, π/d] and can be understood as the fast-time coordinate along a single cavity roundtrip. (In contrast, t corresponds to a slow-time variable describing the evolution of the intra-cavity field over consecutive roundtrips48.) Note also that, in equation (2), the action of the force enters through a time-dependent gauge potential defined by Ft.

Fig. 2: Synthetic band spectroscopy in the non-linear regime.
figure 2

a, Experimental measurements showing the resonator response in the dual (fast-time) space when the mean detuning δ0 (see equation (6)) is changed with F = 0, Ωm = 2π × 0.3 GHz, JEOM = 0.6 rad and Pin = 280 mW (for other parameters, see Methods). b, Evolution of the average intra-cavity power corresponding to a, showing a ‘step’ feature characteristic of CS formation49. c, Simulation results corresponding to the experiments shown in a. The dashed curves in a and c depict the linear band structure \({\delta }_{0}={J}_{{{{\rm{EOM}}}}}\cos ({{{\Omega }}}_{m}\tau )\) associated with the tight-binding Hamiltonian described by equation (1), and tR = FSR−1 is the time it takes for light at the driving frequency to complete one roundtrip. d, Concatenation of optical spectra measured for different cavity detunings, showing the characteristic signatures of modulation instability. e, CS spectrum measured for Pin = 280 mW and a detuning δ0 = 0.64 rad (solid red line) and compared with the linear state with no CS present (Pin = 1 mW, δ0 = 0 rad, dark grey). The dashed lines indicate numerical predictions obtained from the LLE (see ‘Modelling’ section in Methods), while the inset shows the corresponding simulated temporal profile of the CS. Note that only the envelopes of the spectra are shown for the CS and simulations, for clarity.

Source data

Full size image

When F = 0, one identifies the dispersion relation \(E(\tau )\,=\,-2J\cos (d\tau )\), which reveals the existence of a band structure (Fig. 1b, top-right inset, blue). Activating the force (F ≠ 0) generates a constant drift along the momentum (τ) space, hence leading to transport: a localized wave packet experiences an oscillating band velocity dE/dτ, causing the packet to oscillate back and forth along the synthetic frequency lattice, that is, undergo BOs. In this ideal linear framework, the oscillatory motion is characterized by a Bloch period TBO and an oscillation amplitude ABO in the synthetic (frequency) space given by2

$${T}_{{{{\rm{BO}}}}}=\frac{2\pi }{Fd}\quad \qquad \qquad {A}_{{{{\rm{BO}}}}}=\frac{2J}{F}.$$
(3)

The Schrödinger equation associated with equation (1) is useful in revealing the analogy between a quantum particle on a periodic lattice and an optical resonator with an intra-cavity EOM. However, to permit an accurate description of the system under general conditions, the equation must be rigorously augmented with terms that take into account the full effects of non-linearity, group velocity dispersion, driving and dissipation. This yields a driven–dissipative non-linear Schrödinger equation, also known as a Lugiato–Lefever equation (LLE)45,62, that is generalized here to account for the intra-cavity phase modulation (see equation (6)). CSs correspond to steady-state (invariant along t) solutions of the LLE that are localized along the fast-time (τ) coordinate and characterized by a broad comb-like spectrum in the frequency (ω) domain (Fig. 1b). In what follows, we present a series of original experiments that probe their behaviour when JEOM ≠ 0, unveiling Bloch band transport phenomena whose precise features are shaped by the interplay of non-linearity and dissipation (Fig. 1c–e).

Dissipative solitons on a synthetic band structure

Our experiment consists of a 64-m-long ring resonator (yielding an FSR of 3.12 MHz) that is mainly built from standard single-mode optical fibre (Fig. 1a and Methods). The resonator is coherently driven at 1,550 nm using nanosecond, flat-top laser pulses that are synchronized to the FSR of the cavity. The driving pulses are derived from a narrow-linewidth continuous wave (cw) laser and launched into the resonator via a 99/1 coupler.

The synthetic frequency dimension is realized by an intra-cavity EOM that is driven with a radio-frequency signal whose amplitude (JEOM) and frequency (fEOM) can be freely adjusted. Because the EOM introduces considerable losses, which hinders the accumulation of intra-cavity power levels sufficient for the observation of non-linear effects, an erbium-doped fibre (EDF) amplifier is inserted into the cavity. This amplifier partially compensates for the loss due to the EOM55, thus preserving low effective loss (Methods).

The band structure associated with the synthetic frequency dimension can be probed by scanning the mean phase detuning, δ0 (see equation (6)), between the driving laser and a cavity resonance, which is achieved experimentally by sweeping the frequency of the laser that drives the resonator, while simultaneously measuring the evolution of the intra-cavity intensity profile along the fast-time domain. Plotting the intracavity intensity on a 2D diagram with the fast-time coordinate τ as the x axis and δ0 as the y axis then reveals the band (ref. 31 and Methods). Figure 2a shows results from such experiments when the EOM frequency is perfectly synchronized with an integer multiple of the FSR (Δf = 0 ⇒ F = 0).

Similarly to when operating in the linear regime31, the phase modulation induced by the intra-cavity EOM engenders a dynamical modification of the cavity resonance condition along the fast-time domain, thus bending the resonator’s response along the dual space. The dashed curve in Fig. 2a shows that the linear band structure defined through \({\delta }_{0}={J}_{{{{\rm{EOM}}}}}\cos ({{{\Omega }}}_{m}\tau )\) qualitatively follows the observed response, but with deviations owing to the additional effect of non-linearity61. A more conspicuous contrast with the linear theory is the emergence of a localized structure in dual space as δ0 increases beyond the top of the band. This structure corresponds to a CS, emerging spontaneously as the mean detuning δ0 is swept across a resonance (Supplementary Information Sect. E). Note that the emergence of this CS at the top of the band does not correspond to the band soliton coherent structure introduced in ref. 61, which originates from a front pinning effect and thus does not appear relevant for studying transport phenomena.

To gain more insight, Fig. 2c shows results from numerical simulations of the generalized LLE with parameters corresponding to the experimental configuration of Fig. 2a (Methods). The simulations also show clearly the bending of the resonator’s response, as well as the emergence of the CS at the top of the band structure. However, in addition, the simulations also reveal that the band itself exhibits complex internal structures, being composed of highly localized wave packets that fluctuate as δ0 increases. This internal structure stems from a Turing-type modulation instability (MI) that is enabled by the anomalous dispersion of the resonator and breaks the locally quasi-homogeneous intra-cavity field into fast fluctuating wave packets45,46,47. Because the threshold condition of the instability depends upon the cavity detuning (that itself depends upon fast time due to the intra-cavity EOM), this instability remains localized to within the band52,61.

The picosecond-scale internal structure of the band (as well as the precise profile of the CS) is not directly resolved in our experiments (Fig. 2a) due to the finite, 12 GHz bandwidth of our time-domain detection system (Methods). However, measurements made along the synthetic (frequency) space completely corroborate the simulation results. Figure 2d shows the optical spectrum of the intra-cavity field measured across a range of cavity detunings where simulations predict band MI to manifest itself. These measurements reveal a wave packet width in the synthetic (frequency) space of about 200 GHz, commensurate with the simulated picosecond-scale features in the dual (fast-time) space.

Figure 2e shows two measured optical spectra obtained either in the non-linear CS regime (red curve) or below the CS formation threshold (linear regime, dark grey). The CS state is obtained for a driving power of Pin = 280 mW and a cavity detuning of δ0 = 0.64 rad, and is compared with the linear state (Pin = 1 mW, δ0 = 0 rad). The CS spectrum has a sech squared profile with a 3 dB bandwidth of 0.125 THz, corresponding to a 2.6 ps wave packet in duration (Fig. 2e, inset). Because the CS circulates without distortion round trip after round trip, its spectrum consists of sharp discrete lines (a frequency comb) that are equally spaced by the resonator FSR. This equi-spacing of the CS’s spectral lines can be attributed to the cancellation of group velocity dispersion by the solitons’ non-linearity, and is in stark contrast to the linear resonator modes that are not equally spaced due to dispersion—a fact that fundamentally limits the extent of synthetic arrays attainable under linear operation conditions63 (see also Supplementary Information Sect. B). Compounded by its broad spectral width, with more than 128,000 lines above the −20 dB level, the CS state can thus be seen to substantially extend the number of frequency modes (synthetic lattice sites) that are coupled through the intra-cavity modulator, especially when compared with the linear state, which only displays 30 frequency modes above the noise floor.

BOs of cavity solitons

The results shown in Fig. 2 represent the experimental observation of dissipative solitons in the presence of a synthetic frequency dimension. In addition to confirming the salient theoretical descriptions of ref. 61, these results present CSs as a promising, high-resolution tool for the study of Bloch band transport in the presence of non-linearity and dissipation. To probe for such transport, we experimentally introduce an effective force F along the synthetic frequency dimension by slightly detuning the EOM frequency from a harmonic of the cavity FSR (Δf ≠ 0 ⇒ F ≠ 0). We then use an ultrafast dispersive Fourier transform scheme64,65 to record the roundtrip-by-roundtrip evolution of the intra-cavity optical spectrum in a regime where a single CS circulates the cavity (Methods).

Figure 3a–d displays typical trajectories measured in the synthetic (frequency) space for different effective forces F. Here the pseudo-colour plots show a concatenation of CS optical spectra measured on a roundtrip-by-roundtrip basis as the soliton circulates around the ring, hence illustrating the motion of a wave packet along the synthetic lattice. These measurements immediately reveal two qualitatively different regimes. First, for small effective force F (Fig. 3a), the CS experiences a fast transient motion along the synthetic frequency dimension (occurring typically over a few hundred roundtrips and not captured here due to experimental constraints), but eventually comes to a halt at a fixed (synthetic) position (close to 50 GHz in Fig. 3a) that is offset from the soliton’s initial location, when F = 0, corresponding to the carrier frequency of the driving field, centred at 0 GHz. This behaviour is a manifestation of non-linear synchronization: the modulation induced by the EOM pins the CS, shifting its mean frequency so as to cancel the temporal desynchronization between the two (see refs. 50,56,66 for related CS synchronization involving different mechanisms). Note that the absence of spectral oscillations in this weak force regime has been further confirmed experimentally by means of complementary measurements based on an offset filtering technique (Supplementary Information Sect. F).

Fig. 3: BOs of dissipative solitons.
figure 3

a–d, Concatenation of experimentally measured CS optical spectra as a function of time for effective force F and modulation amplitude JEOM values of 0.1 rad and 1.9 × 10−7 (a), 0.1 rad and 2.2 × 10−6 (b), 0.1 rad and 3.0 × 10−6 (c) and 0.05 rad and 3.0 × 10−6 (d), respectively. Each measurement was obtained with Pin = 280 mW, Ωm = 2π × 9.7 GHz and δ0 = 1.5 rad (for other parameters, see Methods). The dash-dotted white line in a shows the theoretical prediction of the synchronization-induced CS frequency offset deduced from the non-linear theory in equation (4), while the dashed curves in b–d show oscillations corresponding to linear and conservative ideal BOs with period and amplitude given by equations (3) (see also section ‘BOs of cavity solitons’ in the main text). e,f, The measured amplitude ABO (e) and period TBO (f) of CS oscillations in the synthetic frequency space as a function of the effective force F (red dots). Panel e also shows the theoretical prediction of equations (4) (dash-dotted pink line) and the experimental result deduced from a (pink dot), highlighting the frequency offset undergone by the CS in the synchronization regime. The blue and red curves in e and f show theoretical predictions from the ideal linear BO (equations (3)) and non-linear (equations (4)) theories, respectively. Note that the error bars (s.d.) related to the uncertainties of measurements of the amplitude and period of BOs are smaller than the red dots in e and f.

Source data

Full size image

In stark contrast, for large effective forces F (Fig. 3b–d), the pinning induced by the modulation is insufficient to cancel the external desynchronization, resulting in the CS exhibiting oscillations in the synthetic (frequency) space. Physically corresponding to periodic red and blue shifting of the solitons’ frequency, these oscillations are analogous to BOs occurring along the systems’ synthetic dimension. Indeed, the dashed curves in Fig. 3b–d show the sinusoidal trajectories with amplitude and period corresponding to the ideal BOs given by equations (3). As can be seen, these theoretical predictions are in excellent agreement with the experimental measurements, confirming that the oscillations experienced by the dissipative CSs for large effective force F can be likened to BOs.

To better understand the transition between the two qualitatively distinct dynamical regimes observed in Fig. 3a–d, we performed experiments over a wide range of effective forces F. Results from these experiments are summarized as red circles in Fig. 3e,f, where we respectively depict the amplitude and period of the oscillations experienced by the solitons in the synthetic (frequency) space. Note that the data in the synchronization regime of Fig. 3e represent constant frequency shift and not an oscillation amplitude. These measurements clearly reveal how the CSs transition from synchronization to oscillations as the effective force F increases, and also how the oscillation characteristics tend towards those predicted by the linear and conservative BO theory (equations (3), blue curve).

All of the experimental results presented in Fig. 3 are in excellent agreement with predictions from the LLE (Methods). Indeed, the red curves in Fig. 3e,f show oscillation characteristics extracted from a non-linear theory derived by applying a Lagrangian perturbative approach to the CS solutions (refs. 67,68 and Supplementary Information Sect. A). This framework yields the following generalized transport equations in the synthetic (frequency) space and the dual (fast-time) domain:

$$\begin{array}{ll}{t}_{{{{\rm{R}}}}}\dfrac{{\mathrm{d}}\langle \omega \rangle }{{\mathrm{d}}t}&=-{{{\varLambda }}}_{{{{\rm{e}}}}}\langle \omega \rangle +{J}_{{{{\rm{EOM}}}}}{{{\varOmega }}}_{m}\sin ({{{\varOmega }}}_{m}\langle \tau \rangle ),\\ {t}_{{{{\rm{R}}}}}\dfrac{{\mathrm{d}}\langle \tau \rangle }{{\mathrm{d}}t}&={t}_{{{{\rm{R}}}}}F+{\beta }_{2}{L}_{\mathrm{c}}\langle \omega \rangle ,\end{array}$$
(4)

where 〈ω〉 and 〈τ〉 represent the CS’s centre of mass along the frequency and fast-time coordinates, respectively, Lc is the resonator circumference, tR = FSR−1, Λe is the effective resonator dissipation expressed as a proportion of the intensity lost each roundtrip and β2 is the group velocity dispersion coefficient of the resonator waveguide.

Additional insights can be obtained by analysing the equations in the limits where F is small and large, respectively. In the former limit (F ≈ 0), the frequency variable 〈ω〉 evolves slowly, being slaved to the adiabatically changing temporal variable 〈τ〉. This allows the approximation d〈ω〉/dt = 0, yielding the following Adler-like synchronization equation56,69 for the temporal variable 〈τ〉 (see also Supplementary Information Sect. A):

$${t}_{{{{\rm{R}}}}}\frac{{\mathrm{d}}\langle \tau \rangle }{{\mathrm{d}}t}=F{t}_{{{{\rm{R}}}}}+{\beta }_{2}{L}_{\rm{c}}\frac{{J}_{{{{\rm{EOM}}}}}{{{\varOmega }}}_{m}}{{{{\varLambda }}}_{{{{\rm{e}}}}}}\sin ({{{\varOmega }}}_{m}\langle \tau \rangle ).$$
(5)

It should be clear that a fixed point exists for 〈τ〉 provided that ∣F∣ < ∣Fc∣ = ∣β2LcJEOMΩm/(ΛetR)∣, in which case the CS will be synchronized to the modulation induced by the EOM, and the soliton’s mean frequency correspondingly pinned to a constant value.

In the opposite limit, ∣F∣tR ≫ ∣β2Lc〈ω〉∣, we have 〈τ〉 ≈ Ft. If additionally ∣F∣ ≫ Λe/(2πm), the solution to the CSs’ position in the synthetic (frequency) space can be written as \(\langle \omega \rangle(t) \approx -{J}_{{{{\rm{EOM}}}}}{{{\varOmega }}}_{m}/(2\uppi mF)\cos ({{{\varOmega }}}_{m}Ft+{\phi }_{0})\), where ϕ0 is a constant phase offset, revealing the expected BO period TBO = 2π/(ΩmF) and amplitude A = JEOMΩm/(2πmF) = 2J/F, in agreement with equation (3).

The analysis above shows that the generalized transport equations (4) well capture the non-linear soliton behaviour for small and large effective force F and that, in the latter limit, the oscillations display characteristics expected for BOs. These equations also reveal the physical mechanism that causes the oscillation characteristics to deviate from ideal BOs in the regime of intermediate force F: the cavity dissipation dampens the oscillations in the synthetic space, leading to an amplitude that is reduced from the conservative limit.

Discussion

We have reported on the generation and manipulation of dissipative solitons in a synthetic frequency dimension. Our experiments were performed in a coherently driven Kerr-type resonator that incorporates an EOM so as to introduce a synthetic 1D (tight-binding) lattice along the frequency axis. We then demonstrated that dissipative Kerr CSs can spontaneously emerge in the resonator when probing the system’s band structure. By detuning the EOM frequency from an integer multiple of the cavity FSR, we implemented an effective force along the synthetic frequency dimension, exploiting the CS state—a natural attractor of the system—for the study of Bloch transport in the presence of non-linearity and dissipation. Our experiments show that, depending on the magnitude of the effective force, the CSs can undergo synchronization or oscillations, with the oscillation characteristics tending towards those attributed to ideal long-lived BOs in the large force limit, a phenomenon that cannot be realized in the absence of CSs (in this system).

Compared with resonator-based systems operating in the linear regime, the unique characteristics of CSs enable one to substantially extend the size of the synthetic 1D tight-binding lattice. Furthermore, the solitons can be used as a highly localized tool to probe the system’s Bloch band structure with unprecedented resolution: while direct band structure spectroscopy (Fig. 2a and ref. 31) can only resolve band features larger than the photo-detector response time, the amplitude of CS BOs—which directly reflect the band structure—is inversely proportional to the width of the Brillouin zone, thus becoming more and more discernible as the band features become smaller. In this context, it is worth noting that the width of the Brillouin zone explored by the CSs in Fig. 3 is an order of magnitude smaller than that of the band probed in Fig. 2, and three orders of magnitude smaller than those studied in ref. 31.

Several extensions of our present work can be envisioned. For example, CSs could permit the study of the impact of non-linearity and dissipation (and more generally, the openness of the system) in high-dimensional synthetic frequency crystals, implemented by driving the intra-cavity EOM with multiple-tone radio-frequency (RF) signals31. Non-Hermitian lattices in the frequency space could be also engineered through simultaneous amplitude and phase modulations of the Kerr resonator38. Finally, more complex synthetic structures with non-trivial topologies could be generated by using multiple coupled or multi-component, modulated cavities33,35,70,71, whereas on-chip systems could be engineered by leveraging state-of-the-art photonic integration36,60,63,72. To conclude, our work establishes that synthetic dimension engineering in Kerr-type optical resonators can be used to study how non-linearity and dissipation affect Bloch band transport, while simultaneously permitting new avenues for the manipulation of dissipative CSs with potential applications in optical frequency comb generation and non-linear topological photonics41.

Methods

Modelling

Accurate modelling of the Kerr cavity dynamics requires that the linear Schrödinger equation associated with equation (1) be rigorously augmented with terms that take into account the full effects of non-linearity, group velocity dispersion, driving and dissipation. This yields the so-called LLE45,62, generalized to account for the intra-cavity phase modulation61:

$$\begin{array}{ll}\mathrm{i}{t}_{{{{\rm{R}}}}}\dfrac{\partial A}{\partial t}&-\dfrac{{\beta }_{2}{L}_{\mathrm{c}}}{2}\dfrac{{\partial }^{2}A}{\partial {\tau }^{2}}+\gamma {L}_{\mathrm{c}}| A{| }^{2}A=\\ &-\mathrm{i}\dfrac{{{{\Lambda }}}_{{{{\rm{e}}}}}}{2}A+\mathrm{i}\sqrt{\theta {P}_{{{{\rm{in}}}}}}+[{\delta }_{0}-{J}_{{{{\rm{EOM}}}}}\cos ({{{\varOmega }}}_{m}(\tau -Ft))]A.\end{array}$$
(6)

Here, A(t, τ) describes the envelope of the intra-cavity electric field in the dual (fast-time) space, Lc is the resonator circumference and tR = FSR−1 is the roundtrip time at the driving wavelength. β2 and γ are respectively the group velocity dispersion and the non-linear Kerr coefficient of the resonator waveguide, Λe denotes the effective cavity loss that takes into account the intra-cavity gain of the optical amplifier55, θ and Pin correspond respectively to the input coupler ratio and the coherent driving power and δ0 is the mean value of the phase detuning between the driving field and a cavity resonance. Note that the LLE is written in a reference frame moving at the group velocity of light at the driving wavelength. In the presence of a desynchronization between the EOM frequency and an integer multiple of the cavity FSR (Δf ≠ 0 ⇒ F ≠ 0), the modulation imparted by the EOM drifts in this reference frame. On the other hand, by shifting the reference frame such that τ → τ − Ft, we obtain the following modified LLE where the modulation is stationary:

$$\begin{array}{ll}\mathrm{i}{t}_{{{{\rm{R}}}}}\dfrac{\partial A}{\partial t}&-\mathrm{i}{t}_{{{{\rm{R}}}}}F\dfrac{\partial A}{\partial \tau }-\dfrac{{\beta }_{2}{L}_{\mathrm{c}}}{2}\dfrac{{\partial }^{2}A}{\partial {\tau }^{2}}+\gamma {L}_{\mathrm{c}}| A{| }^{2}A=\\ &-\mathrm{i}\dfrac{{{{\Lambda }}}_{{{{\rm{e}}}}}}{2}A+\mathrm{i}\sqrt{\theta {P}_{{{{\rm{in}}}}}}+[{\delta }_{0}-{J}_{{{{\rm{EOM}}}}}\cos ({{{\varOmega }}}_{m}\tau )]A.\end{array}$$
(7)

By retaining only the first two terms (the last term) on the left-hand side (right-hand side) of equation (7) and applying the Fourier transformation, one obtains the linear Schrödinger equation associated with equation (1) (Supplementary Information Sect. A).

The simulation results shown in Fig. 2 were obtained by numerically integrating equation (7) using the split-step Fourier method with parameters corresponding to the experiments: Lc = 64 m, γ = 10−3 W−1 m−1, β2 = −20 × 10−27 s2 m−1, Λe = 0.05, θ = 0.1, Pin = 0.28 W, JEOM = 0.6 rad and fEOM = 0.3 GHz. The simulations shown in Fig. 2e used a hyperbolic secant initial condition with the mean detuning fixed at δ0 = 0.64 rad. The simulations shown in Fig. 2c were obtained with a noisy initial condition and with the mean phase detuning δ0 linearly increasing at a rate of 66.5 mrad per roundtrip, and by replacing the effective loss Λe in the right-hand side of equation (7) by \([{{\varLambda }}-{G}_{0}/(1+{P}_{{{{\rm{sat}}}}}^{-1}\langle | A{| }^{2}\rangle )]\) to take into account for the intracavity amplifier saturation, where 〈∣A∣2〉 is the average intracavity power, G0 = 0.47 is the unsaturated gain, Psat = 280 mW is the amplifier saturation power and Λ = 0.52 dB is the intrinsic cavity loss55.

Experimental set-up

The resonator schematically displayed in Fig. 1a is made of ~63 m of standard telecommunication single-mode fibre (SMF-28) spliced to a 75-cm-long segment of EDF (Liekki ER16-8/125), leading to a cavity FSR of 3.12 MHz (see also Supplementary Information Sect. C). The amplifying section provides the optical gain required to partially compensate for the cavity roundtrip losses (close to 3.2 dB). The length of the amplifying section has been carefully adjusted following the method described in ref. 55. The EDF is surrounded by two wavelength division multiplexers (WDMs) to combine the 1,480 nm backward pump with the intra-cavity signal and to reject the residual non-absorbed pump power. When the EDF is removed from the resonator, the total losses of the cavity have been evaluated to be 3.2 dB, which corresponds to a resonance linewidth of 390 kHz (intrinsic finesse \({{{\mathcal{F}}}}=8\), Q factor of 750 × 106). With the EDF, the effective finesse is \({{{{\mathcal{F}}}}}_{\mathrm{e}}=125\) (Q factor of 7.8 × 109) and the linewidth is about 25 kHz. A 99/1 tap coupler is used to inject the coherent driving beam into the cavity, while part of the intra-cavity power is extracted for analysis thanks to a 90/10 coupler. Before the input coupler, a polarization controller is used to align the polarization state of the driving beam along one of the two polarization eigenmodes of the cavity. The synthetic dimension is implemented in the frequency domain using a commercial phase modulator (EOM, bandwidth 12 GHz), inserted directly into the ring resonator. The EOM is driven by an RF signal generator whose amplitude (JEOM, experimentally limited to 0.6 rad) and frequency (fEOM) can be freely adjusted. In addition, an intra-cavity polarization controller limits the EOM polarization-dependent losses.

The resonator is coherently driven by means of a sub-100-Hz linewidth cw laser, slightly tunable and centred at 1,550.12 nm. At this driving wavelength, the overall resonator displays anomalous group velocity dispersion—a requisite for CS existence. The cw laser is modulated by means of a Mach–Zehnder amplitude modulator (bandwidth 12 GHz, extinction ratio 30 dB), driven by a pulse pattern generator synchronized with the cavity FSR, so as to generate a train of 1.2 ns square pulses. The resulting flat-top pulse train is then amplified with a commercial EDF amplifier before injection into the ring resonator.

We probe the band structure by slowly increasing the driving laser wavelength and recording the power at the output of the 90/10 coupler with a 200 kHz photodiode (Fig. 2b) or with a 12 GHz detection system (Fig. 2a), as described below. The cavity can be stabilized at any detuning δ0 by means of a counter-propagating and frequency-shifted control signal73. This signal is generated by extracting 5% of the driving cw laser and sending it to a tunable opto-acoustic frequency shifter (110 ± 5 MHz). The resulting low-power (0.1 mW) control signal is then injected into the cavity on the same polarization state as the main signal thanks to an optical circulator combined with a polarization controller. The cavity detuning is stabilized through feedback on the driving cw laser wavelength so as to maintain a constant intra-cavity average power for the control signal. The feedback signal is generated by a proportional–integral–derivative controller, driven by a 200 kHz photodiode. We then map the detuning to the frequency of the control signal by fitting the cavity transmission in the linear regime. Finally, at the output of the system, the intra-cavity field is characterized in both the temporal and spectral domains by means of a 45 GHz photodiode connected to a 12 GHz real-time oscilloscope (20 Gsamples s−1) and an optical spectrum analyser, respectively.

BOs

The CS evolution along the synthetic space is recorded roundtrip-by-roundtrip by performing a dispersive Fourier transformation (DFT)64,65. Using two 50-km-long spools of standard single-mode fibre (SMF-28, β2 = −20 × 10−27 s2 m−1), our real-time spectrum measurements reach a resolution of 12 GHz (ref. 5), which imposes an upper limit for the desynchronization force used in our experiments of around F = 1.25 × 10−5 so as to efficiently resolve the spectral BOs. To cope with propagation losses (10 dB per spool), each spool is surrounded by two WDMs (1,450/1,550 nm) to perform (co-propagating) Raman amplification. The 1,450 nm Raman pump power, before being split in two, is set to 1.4 W. Before the DFT, to avoid the detrimental interferences occurring between the CS and its associated cw background, a non-linear optical loop mirror (NOLM) has been implemented to remove the cw component. The NOLM is made of a fibre loop closed on a 50/50 coupler and includes a variable optical attenuator, 200 m of dispersion/compensating fibre (non-linearity coefficient γDCF = 3 W−1 km−1) and a polarization controller. When the variable optical attenuator is set to 5%, the NOLM transmission reaches almost 1 for a CS of 50 W peak power, whereas its cw background is attenuated by 20 dB (ref. 74). A commercial EDF amplifier is used at the input of the NOLM to increase the CS peak power above 50 W. As the amplitude of CS BOs depends on the EOM frequency, the latter is set close to Ωm = 2π × 9.7 GHz to be sufficiently above the DFT resolution (12 GHz). Finally, BOs of CSs are recorded while slowly scanning the cavity detuning in the vicinity of δ0 = 1.5 rad. This scan is so slow that the detuning can be considered constant over the duration of the measurements shown in Fig. 3. Note also that the initial phase shifts observed in Fig. 3b–d are purely arbitrary as they only correspond to the different starting points of the recording process. A complete experimental set-up is given in the Supplementary Information Sect. C.

We note that Bloch oscillations were recently detected along a synthetic dimension of atomic harmonic trap states75.