Main

A quantum modular architecture is a distributed network (Fig. 1a) of modules that communicate with one another through quantum and classical channels. Each module is a small quantum processor that is composed of two separately optimized subsystems (Fig. 1b): data qubits that store and process quantum information and are realized as quantum memories; and communication qubits that mediate interactions between different modules. Each module operates individually as a highly functional node, capable of performing intra-module operations between the data and communication qubit subsystems. Inter-module operations between the data qubits are enabled by distributing entanglement between communication qubits. By adopting this modular approach, the data qubit subsystems are well-isolated from the other modules, which provides a systematic strategy for minimizing crosstalk and residual interactions across the entire network even when the system is scaled up. So far, elementary quantum networks have demonstrated the transmission of quantum information and the generation of entanglement between communication qubits8,9,10,11. To extend the computational capabilities of these networks for universal quantum computation, it will be necessary to implement entangling operations on data qubits across different modules.

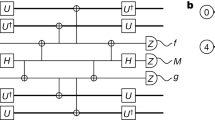
Fig. 1: Construction of a modular architecture and teleported CNOT gate.
figure 1

a, Network overview of the modular quantum architecture. Modules are represented as nodes of a quantum network and are composed of data qubit(s) (magenta) and communication qubit(s) (cyan). Coupling between modules is generated through reconfigurable communication channels that may be enabled (dark purple lines) or disabled (light purple lines). b, Quantum modules. Each module houses a small quantum processor that is capable of high-fidelity operations among data qubits and communication qubits. In our experiment, we create two modules, each consisting of one data qubit (D1 and D2) and one communication qubit (C1 and C2). c, Teleported CNOT circuit between D1 and D2. The teleported CNOT circuit requires: (1) entanglement between C1 and C2 (purple meander), (2) local operations, (3) measurement of C1 in the \(\hat{Z}\) basis and C2 in the \(\hat{X}\) basis, where \(\hat{X}\) and \(\hat{Z}\) are Pauli operators, and (4) classical communication (double lines) and feedforward operations. d, Experimental realization (schematic top view) in a three-dimensional circuit-quantum-electrodynamics implementation. Each module consists of a data qubit defined as a coaxial quarter-wavelength (λ/4) three-dimensional cavity (magenta), a communication qubit defined as a Y-shaped transmon qubit (cyan) and a Purcell-filtered, quasi-planar, λ/2 stripline readout resonator (black). In this experiment, the two modules are linked by an additional mode realized as a coaxial λ/4 three-dimensional cavity (purple) that serves as a bus mode (Extended Data Fig. 1, Supplementary Information).

Full size image

Owing to the inherent isolation between modules, multi-qubit operations in the modular architecture cannot be implemented using conventional approaches that rely on direct interactions, but instead utilize quantum teleportation3,12. State teleportation was initially proposed12 and later experimentally demonstrated13,14,15,16,17,18,19 as a technique for transferring an unknown quantum state between two quantum systems without transmitting the physical system that encodes the quantum state. This protocol relies on shared entanglement as a resource, along with local operations and classical communication between the two systems. Together these elements form the distinguishing characteristics of teleportation-based protocols in which information is transmitted through distinct quantum and classical channels. Expanding on this technique, the teleportation of a two-qubit quantum gate implements a unitary operation between two unknown states with a protocol that obviates the need for any direct interaction between the two data qubits (Fig. 1c)3,4,5,20. Similar protocols have been demonstrated previously between two physical data qubits without real-time classical communication21,22,23, with the desired operation extracted probabilistically through post-selection. However, to avoid excessive overhead and to make the modular approach scalable, it is crucial to perform these teleported gates deterministically.

In our work, we demonstrate a teleported CNOT gate that is deterministic and operates on logically encoded data qubits. A logical qubit is a two-dimensional subspace encoded within a higher-dimensional space designed with symmetry properties that allow for the detection and correction of certain errors. We implement two modules that each consist of a superconducting microwave cavity as the data qubit and a transmon as the communication qubit. Here, we generate entanglement between communication qubits via a local quantum bus that individually couples to each communication qubit. Our implementation can be adapted in the future to incorporate schemes for generating remote entanglement11,24, which will be necessary for a scalable quantum modular architecture. We use a hardware-efficient approach6,25 to logically encode each data qubit within the states of a long-lived cavity mode. Importantly, despite the added complexity of our logical encoding, we implement high-fidelity control over both the data and communication qubit within each module. Using the teleported CNOT gate combined with real-time adaptive control, we generate a Bell state between two logical qubits and characterize the logical quantum process, thus validating our entangling operation on logical qubits.

Our physical implementation capitalizes on highly coherent and controllable elements from the three-dimensional circuit-quantum-electrodynamics platform. Each module (Fig. 1d, Methods) consists of a high-quality-factor (high-Q) three-dimensional electromagnetic cavity26 as the data qubit, a transmon qubit as the communication qubit and a Purcell-filtered, low-Q stripline resonator27 for readout of the transmon qubit. The transmon qubit is capacitively coupled to both the data qubit and the readout resonator. We achieve data qubit lifetimes (of about 1 ms) that are around three orders of magnitude greater than the measurement time (less than about 1 μs), enabling both quantum information storage and fast measurement within a single package (Supplementary Information). In this experiment, the communication channel is implemented as an additional cavity mode and functions as a quantum bus (hereafter, ‘bus’), coupling individually to both communication qubits. Although we utilize this local mode to link the two modules, the two data qubits have an immeasurably small direct coupling, which is bounded to be at least an order of magnitude smaller than the smallest decay rate in our system (Supplementary Information). Therefore, despite the physical proximity (around 2 cm) between the two modules, our two data qubits are effectively non-interacting, demonstrating the same isolation distinctive of remote modular architectures. In addition, our entire device exhibits low readout crosstalk, which is critical for the teleported gate and is another characteristic property of independent modules (Methods).

The high-dimensional cavity modes that define our data qubits allow for a wide range of encodings, including those that can address the dominant errors that face cavity memories6,25. For our data qubits to fulfil the role of a quantum memory, we chose to encode each data qubit using the first-level bosonic binomial quantum code25, which has logical basis states (specified in the photon-number basis of the cavity)

$$| {0}_{{\rm{L}}}\rangle =| 2\rangle ,\hspace{2pt}| {1}_{{\rm{L}}}\rangle =\frac{| 0\rangle +| 4\rangle }{\sqrt{2}}$$

Our protocol is flexible to different data-qubit encodings, and we also present results using the \(| 0\rangle \) and \(| 1\rangle \) Fock basis, which requires only an in situ software modification to the control pulses. The first-level binomial encoding specifies a logical qubit that can be used to detect and correct for single-photon loss, the main error mechanism for cavity memories (Methods)6. Demonstration of the teleported gate using such a logical encoding offers a practical route for incorporating quantum error-correction protocols in the future. As an illustration of our control of the logical qubit, we prepared six cardinal states of the logical Bloch sphere and characterized each state by measuring the Wigner function of the data qubit (Fig. 2a). The Wigner function not only provides a strikingly visual representation of the logical qubit state, but also completely specifies the underlying cavity state, a capability analogous to full state tomography of the constituent physical qubits that compose a logical qubit.

Fig. 2: Logical data-qubit encoding and CNOT truth table.
figure 2

a, Logical Bloch sphere for the binomial code encoding. The data qubit is logically encoded in the binomial code basis and the Wigner function for each of the six cardinal states \(\{\pm {\hat{Z}}_{{\rm{L}}},\pm {\hat{X}}_{{\rm{L}}},\pm {\hat{Y}}_{{\rm{L}}}\}\) is shown (colour scale as in b). b, Teleported CNOT truth table. The left two columns show experimental Wigner functions for all four logical computational states as input states, and the right two columns show the extracted Wigner functions after performing the teleported CNOT operation, illustrating the correct classical behaviour of the gate. We determine the scaled Wigner function by directly measuring the displaced joint parity of the cavity, which is parameterized by β, a complex variable of the cavity state.

Full size image

The teleported CNOT gate starts with the generation of entanglement in the communication qubits to create a communication channel between the two modules (step 1 in Fig. 1c). Any maximally entangled state is acceptable, and the specific choice requires only small modifications to later steps of the teleported-gate protocol. In our implementation, we use the Bell state \(| {\Psi }^{+}\rangle =(| ge\rangle +| eg\rangle )/\sqrt{2}\), where \(| g\rangle \) and \(| e\rangle \) are the ground and first excited states, respectively, of the transmon qubits and specify the basis states of the communication qubits. The state is generated by performing a resonator-induced phase (RIP) gate28 on the bus and single-qubit rotations on the communication qubits (Methods). Using this gate, we generated a Bell pair between the communication qubits in approximately 680 ns with a state fidelity of 97% ± 1% as determined from quantum state tomography (Methods; the error quoted here and elsewhere is defined in Methods and Supplementary Information).

Next, local operations performed within each module entangle the data and communication qubits (step 2 in Fig. 1c). Our local operations are implemented using optimal-control techniques, which enable universal quantum control between the data and communication qubits29. We generate all of our local operations with pulse lengths between 1 μs and 2 μs. Characterization of these logical operations yields single-data-qubit and two-qubit (between the data and communication qubits) gate fidelities of around 97% and 94%, respectively (Supplementary Information).

After the entangling local operations, we perform measurements on the communication qubits (step 3 in Fig. 1c), thereby effecting a unitary operation between only the two data qubits. It is essential that the measurements do not reveal information about the state of the data qubits. In the teleported-gate protocol, this is accomplished by individual measurements of the communication qubits in the \(\hat{Z}\) and \(\hat{X}\) bases (where \(\hat{Z}\) and \(\hat{X}\) are Pauli operators), which lead to four uniformly distributed outcomes. Each outcome heralds a unitary operation between the two data qubits that is a CNOT gate up to single-qubit operations. As a result, high-fidelity measurements are necessary to correctly determine the particular operation enacted on the data qubits. In our system, we achieve single-shot state-assignment fidelities of the communication qubits of around 99% (Methods).

Finally, ensuring that the protocol implements the desired CNOT operation independently of the measurement outcome requires classical communication and feedforward operations (step 4 in Fig. 1c). Two classical bits of information are needed to communicate measurement results between modules. This information is used to apply feedforward operations, transforming the protocol into a deterministic operation and thus completing the teleportation. In our experiment, the measurements must be non-destructive to the communication qubits because these qubits are used for subsequent steps of our protocol. To enable the measurements and the feedforward operations, we use a real-time controller6 to orchestrate quantum programs for our experiment, combining control, measurement, state estimation and feedforward in a single integrated system. For every experimental run, this controller handles the distribution of classical information between the two modules and the application of the feedforward operations, all within a fraction of the lifetime (about 1%) of the communication qubits. We independently analysed the measurement and feedforward processes to have a combined fidelity of approximately 97%, excluding the conditional data-qubit operations (Methods).

Therefore, by consuming a shared entangled pair and communicating two classical bits of information, this procedure effects a CNOT operation between the data qubits without requiring a unitary operation between the two modules after the generation of the shared entangled pair. Having demonstrated all of the elements necessary for realizing the teleported CNOT gate, we characterized the full two-qubit gate through a series of four separate analyses.

In the first analysis, we verified the classical behaviour of the gate by generating a truth table for the set of computational states. We prepared the data qubits each of the four states \(\{| {0}_{{\rm{L}}}{0}_{{\rm{L}}}\rangle ,| {0}_{{\rm{L}}}{1}_{{\rm{L}}}\rangle ,| {1}_{{\rm{L}}}{0}_{{\rm{L}}}\rangle ,| {1}_{{\rm{L}}}{1}_{{\rm{L}}}\rangle \}\) and enacted the teleported CNOT on each, ideally leading to the output states \(\{| {0}_{{\rm{L}}}{0}_{{\rm{L}}}\rangle ,| {0}_{{\rm{L}}}{1}_{{\rm{L}}}\rangle ,| {1}_{{\rm{L}}}{1}_{{\rm{L}}}\rangle ,| {1}_{{\rm{L}}}{0}_{{\rm{L}}}\rangle \}\)  . We extracted the input and output states by measuring Wigner functions for each data qubit. Our results (Fig. 2b) provide qualitative validation of the teleported CNOT gate on the computational basis states.

In the second analysis, we demonstrated that our gate is a distinctly quantum operation by using the teleported CNOT gate to generate entanglement between two logical qubits. We prepared the data qubits in the separable initial state \(| {\psi }_{{\rm{init}}}\rangle =(| {0}_{{\rm{L}}}\rangle +| {1}_{{\rm{L}}}\rangle )| {0}_{{\rm{L}}}\rangle /\sqrt{2}\) and performed the gate. The ideal output state is the Bell state \(| {\Phi }_{{\rm{L}}}^{+}\rangle =(| {0}_{{\rm{L}}}{0}_{{\rm{L}}}\rangle +| {1}_{{\rm{L}}}{1}_{{\rm{L}}}\rangle )/\sqrt{2}\). We verified that our teleported CNOT gate generates this logical-qubit Bell pair using two separate methods, which together highlight our ability to characterize the data qubits on a logical level (the encoded two-dimensional subspace) and on a physical level (the multi-dimensional cavity state).

In the first method, we performed a pair of experiments to show that the state exhibits quantum correlations. Given the target state \(| {\Phi }_{{\rm{L}}}^{+}\rangle \), when we measure the control qubit in the logical \({\hat{Z}}_{{\rm{L}}}\) basis and find it in \(| {0}_{{\rm{L}}}\rangle \) \(\left(| {1}_{{\rm{L}}}\rangle \right)\), we expect the target qubit to be \(| {0}_{{\rm{L}}}\rangle \) \(\left(| {1}_{{\rm{L}}}\rangle \right)\). We enacted the logical \({\hat{Z}}_{{\rm{L}}}\) measurement and, conditioned on the result, performed physical-qubit tomography on the target data qubit by measuring its Wigner function (Methods). As expected, we observed strong \(\hat{Z}\) correlations between the control and target data qubits (Fig. 3a, top). Next, we rotated the measurement basis and performed \({\hat{X}}_{{\rm{L}}}\) measurements of the control data qubit. Conditioned on the control data qubit in the state \(| \pm {X}_{{\rm{L}}}\rangle =(| {0}_{{\rm{L}}}\rangle \pm | {1}_{{\rm{L}}}\rangle )/\sqrt{2}\), we experimentally found the target data qubit to be in the expected state \(| \pm {X}_{{\rm{L}}}\rangle \) (Fig. 3a, bottom), thus establishing \(\hat{X}\) correlations between the two data qubits. These two complementary experiments confirm the non-classical nature of the experimental logical Bell state and indicate that our gate produced a non-separable two-qubit state.

Fig. 3: Generation of a logical Bell state.
figure 3

a, Quantum correlations of a logical Bell state. The logical Bell state \(| {\Phi }_{{\rm{L}}}^{+}\rangle =(| {0}_{{\rm{L}}}{0}_{{\rm{L}}}\rangle +| {1}_{{\rm{L}}}{1}_{{\rm{L}}}\rangle )/\sqrt{2}\) is first created using the teleported CNOT gate. The control qubit (D1) is measured in either the logical \({\hat{Z}}_{{\rm{L}}}\) basis (top) or \({\hat{X}}_{{\rm{L}}}\) basis (bottom), and Wigner tomography is performed on the target qubit (D2), conditioned on the measurement result m of the control qubit, m = 0 (left) or m = 1 (right). When measuring in the \({\hat{Z}}_{{\rm{L}}}\) basis (top), a measurement result of m = 0 (m = 1) indicates that the control qubit is found to be in \(| +{Z}_{{\rm{L}}}\rangle \) (\(| -{Z}_{{\rm{L}}}\rangle \)) and the target qubit in \(| +{Z}_{{\rm{L}}}\rangle \) (\(| -{Z}_{{\rm{L}}}\rangle \)). When measuring in the \({\hat{X}}_{{\rm{L}}}\) basis (bottom), a measurement result of m = 0 (m = 1) indicates that the control qubit is found to be in \(| +{X}_{{\rm{L}}}\rangle \) (\(| -{X}_{{\rm{L}}}\rangle \)) and target qubit in \(| +{X}_{{\rm{L}}}\rangle \) \(\left(| -{X}_{{\rm{L}}}\rangle \right)\). Correlations between the measurement result and the measured state indicate the generation of an entangled state between D1 and D2. b, Logical state tomography. After generating \(| {\Phi }_{{\rm{L}}}^{+}\rangle \), logical qubit tomography is performed on both the control and the target qubit. The reconstructed state, represented in the Pauli basis {I, X, Y, Z}, confirms that the teleported CNOT gate has generated the target Bell state, except for reduced contrast from the ideal value. The reconstructed states shown in blue correspond to two-qubit correlations, those in red and green to single-qubit correlations and that in grey to the identity.

Full size image

In the second method, we analysed the joint state within the logical subspace of the two data qubits by performing quantum state tomography (Methods). We reconstructed the two-qubit state in the Pauli basis (Fig. 3b), extracting a state fidelity of \({{\mathscr{F}}}_{{\rm{Bell}}}\) = 68% ± 1% and concurrence of \({\mathscr{C}}\) = 0.37 ± 0.01, which exceeds the threshold for a classically correlated state. These quantities include imperfections associated with logical-state preparation and decoding operations, which together contribute about 6% infidelity for each data qubit. Using the teleported CNOT gate, we have thus generated a Bell state between logical qubits encoded as multi-photon states that, from inspection of the reconstructed density operator, has dominant two-qubit correlations (for example, two-qubit parity \(\langle ZZ\rangle \) = 0.57) and near-zero single-qubit correlations (for example, the single-qubit Z correlations for D1 and D2 are \(\langle ZI\rangle \) = 0.04 and \(\langle IZ\rangle \) = 0.01, respectively).

Our implementation of the teleported gate as a deterministic operation requires reliable classical communication and feedforward operations. In the third analysis, we investigated the importance of classical communication by performing the previously described entanglement sequence, recording the measurement outcomes and extracting four conditioned output states. We performed this sequence with and without applying the feedforward operations (step 4). Each measurement outcome {00, 01, 10, 11} ideally occurs with probability 1/4 and, without the feedforward operations, heralds one of four Bell states \(\{| {\Psi }_{{\rm{L}}}^{+}\rangle ,| {\Psi }_{{\rm{L}}}^{-}\rangle ,| {\Phi }_{{\rm{L}}}^{+}\rangle ,| {\Phi }_{{\rm{L}}}^{-}\rangle \}\), where \(| {\Psi }_{{\rm{L}}}^{\pm }\rangle =(| {0}_{{\rm{L}}}{1}_{{\rm{L}}}\rangle \pm | {1}_{{\rm{L}}}{0}_{{\rm{L}}}\rangle )/\sqrt{2}\) and \(| {\Phi }_{{\rm{L}}}^{\pm }\rangle =(| {0}_{{\rm{L}}}{0}_{{\rm{L}}}\rangle \pm | {1}_{{\rm{L}}}{1}_{{\rm{L}}}\rangle )/\sqrt{2}\) . Our results (Fig. 4a; top, first four panels) are consistent with the ideal outcome, save for reduced contrast, and we extracted conditioned fidelities of {69%, 66%, 69%, 66%} and outcome frequencies of {0.25, 0.26, 0.24, 0.25}. The fact that we generated different Bell pairs indicates that each conditional operation is a CNOT gate up to single-qubit operations. Without real-time knowledge of these measurement outcomes, these states will all add incoherently, resulting in a completely mixed state in which all information has been lost (Fig. 4a; top, ‘All’). If we instead post-selected on the measurement outcomes, the operation would be left as a probabilistic two-qubit gate, achieving the target operation only 1/4 of the time (Fig. 4a; top, measurement outcome 10). Therefore, it is only when we combine real-time classical communication and feedforward that we can implement a deterministic teleported operation that performs the correct process for all measurement outcomes (Fig. 4a, bottom).

Fig. 4: Demonstration of a deterministic teleported CNOT gate.
figure 4

a, Effect of feedforward operations. The teleported CNOT gate is applied to the initial state \(| {\psi }_{{\rm{init}}}\rangle =(| {0}_{{\rm{L}}}\rangle +| {1}_{{\rm{L}}}\rangle )| {0}_{{\rm{L}}}\rangle /\sqrt{2}\) and the fidelity of the resulting state to each of the four Bell states is extracted. When feedforward operations are not applied (top), each measurement outcome {00, 01, 10, 11} results in a different Bell state. If all measurement results are compiled together, the resulting state is completely mixed (‘All’). On the other hand, if the feedforward operations are applied (bottom), then the correct state \(| {\Phi }^{+}\rangle \) is found for every measurement outcome. b, Quantum process tomography of the teleported CNOT gate. We represent the quantum process \({{\mathscr{R}}}_{{\rm{CNOT}}}\) in the Pauli transfer representation, in which the process map is expressed in the Pauli basis: \({{\boldsymbol{P}}}_{{\rm{out}}}={{\mathscr{R}}}_{{\rm{CNOT}}}{{\boldsymbol{P}}}_{{\rm{in}}}\), given input- and output-state Pauli vectors Pin,out (Methods). Agreement between the experimentally reconstructed (left) and ideal (right) processes indicates the successful implementation of a deterministic teleported CNOT gate.

Full size image

Finally, in the fourth analysis, we fully characterized the logical process for the teleported CNOT gate. We performed quantum process tomography on the two logical qubits and our reconstructed process agrees qualitatively with the expected process (Fig. 4b). From the experimental reconstruction, we calculate a process fidelity of \({{\mathscr{F}}}_{{\rm{pro}}}\) = 68% ± 2% without accounting for logical encoding or decoding steps that subtract from the extracted gate fidelity. With these corrections included (Supplementary Information), we infer a process fidelity of \({{\mathscr{F}}}_{{\rm{gate}}}\) = 79% ± 2% for our teleported CNOT gate. To evaluate the experimental performance of the teleported gate, we assembled an error budget that combines the infidelity of each element of the gate, accounting for the known imperfections of our system. From this analysis (Supplementary Information), we expect a gate fidelity of \({{\mathscr{F}}}_{{\rm{thy}}}\) ≈ 84% ± 3%, which is consistent with experimental results. This indicates that other non-idealities, such as residual interactions or imperfect system characterization, are smaller effects in our system. We also performed the teleported operation using the Fock \(| 0\rangle \) and \(| 1\rangle \) states, achieving a process fidelity of \({{\mathscr{F}}}_{{\rm{gate}}}\) = 86% ± 2% when accounting for the encoding and decoding steps. This difference in process fidelity is well understood: the binomial encoding has a higher average photon number \(\left(\bar{n}=2\right)\) compared to the Fock encoding \(\left(\bar{n}=0.5\right)\), which results in an additional overhead in the photon loss rate and increased complexity of the local operations. Although the fidelity of the binomial encoding is lower than that of the Fock encoding, the advantage of the binomial encoding is that a single-photon loss event can, in principle, be detected via parity measurements and is therefore a correctable error.

The performance of our teleported gate, although an encouraging step towards operations between logical qubits, requires improvement to be useful for the modular quantum architecture. An advantage of our work is that the teleported gate is modular and uses relatively modest elements, all of which are part of the standard toolbox for quantum computation in general. Therefore, on-going progress to improve any of the elements will directly increase gate performance. There already exist well-defined prescriptions to improve each element of the teleported gate. For example, a communication qubit implemented using a high-Q cavity instead of a transmon qubit would directly address the dominant source of infidelity in our implementation—the communication-qubit coherence time of T2 ≈ 15 μs. Such a modification would not only enable the development of a module containing error-correctable data and communication qubits, but also introduce opportunities to improve intra-module operations via multi-cavity gates30 and communication-qubit measurements via robust, repeated readout strategies of a bosonic mode5,31.

The protocol for the teleported CNOT gate used in this work is one example of an extensive family of two-qubit operations that may be implemented using the same resources3,4,5. Such teleportation-based gates are important primitives for the implementation of a modular architecture and may be part of a broader approach to fault-tolerant quantum computation2,3,32. One of the next steps will be to demonstrate non-local teleported gates using spatially separate modules, which will require remote entanglement. Because this entanglement can be prepared before the teleported operation, the gate is agnostic to how the entanglement is generated. Therefore, the protocol can take advantage of various approaches, including deterministic33 and probabilistic34 schemes, and should benefit from entanglement-purification protocols5,35. Building on our results and recent demonstrations of remote entanglement in circuit-quantum-electrodynamics systems11,24, it should be possible to integrate these technologies, enabling the development of modular quantum computing using superconducting qubits.

Methods

Experimental device and setup

Our experiment uses three high-Q λ/4 coaxial three-dimensional cavities machined out of a single block of aluminium (99.99% purity) and two sapphire chips on which a Y-shaped transmon qubit and a quasi-planar λ/2 readout resonator are lithographically defined (Extended Data Fig. 1). The device is cooled to T ≈ 10 mK in a dilution refrigerator. Our control hardware includes an FPGA-based controller that functions both as a real-time arbitrary-waveform generator and a digitizer for performing measurements of the system. These measurements are enabled through the use of two independent readout chains that each include a Josephson parametric converter (JPC) for nearly quantum limited amplification of output signals. More detailed information regarding device construction and cryogenic wiring is provided in Supplementary Information.

Transmon measurement

In this experiment, each module is connected to a separate JPC for fast, high-fidelity measurement of the transmon qubit. We achieve single-shot assignment fidelities of around 99.4%, largely limited by transmon decay during the measurement pulse of 600 ns. We define the assignment fidelity as the average probabilities of correctly assigning the state when we prepare the transmon in \(| g\rangle \) and \(| e\rangle \): \({{\mathscr{F}}}_{{\rm{assign}}}=\left[Pr\left( \mbox{`} g\mbox{'}| \hspace{2.77626pt}\left|g\right\rangle \right)+Pr\left( \mbox{`} e\mbox{'}| \hspace{2.77626pt}\left|e\right\rangle \right)\right]/2\). This high-quality measurement, coupled with the real-time capabilities of our quantum controller, enables conditional operations based on an extracted measurement result. The length of time from the start of a measurement pulse to the application of a conditioned operation is around 1,000 ns, which includes the length of the measurement pulse (600 ns), cable delays (200 ns), and integration and state-estimation latencies (200 ns).

It is critical that the two communication qubit measurements be independent for the demonstration of the teleported gate. To assess the measurement crosstalk, we perform a Rabi experiment and simultaneous measurements on both communication qubits (Extended Data Fig. 2a). Our results (Extended Data Fig. 2b, c) indicate that the measurements are highly selective to the qubit addressed. From our data, we estimate the measurement crosstalk—defined to be the ratio of the measurement contrast of measuring the directly coupled qubit to that of measuring the isolated qubit—to be less than 10−4. In future implementations of this experiment in which the two modules are physically separate, the measurement crosstalk will be completely negligible.

Data-qubit encodings

Binomial encoding

As discussed in the main text, we demonstrate the teleported gate using one of the binomial quantum codes25, with basis states \(| {0}_{{\rm{L}}}\rangle =| 2\rangle \) and \(| {1}_{{\rm{L}}}\rangle =(| 0\rangle +| 4\rangle )/\sqrt{2}\). This logical encoding provides the ability to perform quantum error correction against single photon-loss events (for example, the application of the harmonic-oscillator lowering operator \(\hat{a}\)), which is the dominant error mechanism for a cavity functioning as a quantum memory. A photon-loss event on a quantum state \(\left|{\psi }_{{\rm{L}}}\right\rangle =\alpha \left|{0}_{{\rm{L}}}\right\rangle +\beta \left|{1}_{{\rm{L}}}\right\rangle \) transforms this state to \(\left|{\psi }_{{\rm{E}}}\right\rangle =\hat{a}\left|{\psi }_{{\rm{L}}}\right\rangle =\alpha \left|{E}_{0}\right\rangle +\beta \left|{E}_{1}\right\rangle \), with error codewords \(\left|{E}_{0}\right\rangle =\left|1\right\rangle \) and \(\left|{E}_{1}\right\rangle =\left|3\right\rangle \). The quantum amplitudes α and β are left unchanged despite the loss event. Detecting this single-photon error is straightforward because it results in a photon-number parity flip from even to odd, which is readily measured in our circuit-quantum-electrodynamics system using photon-number parity measurements36. Upon detection of an error event, in principle, a correction unitary operator can be applied that takes \(\left|{E}_{0}\right\rangle \to \left|{0}_{{\rm{L}}}\right\rangle \) and \(\left|{E}_{1}\right\rangle \to \left|{1}_{{\rm{L}}}\right\rangle \), preserving the relative quantum amplitudes α and β.

Fock encoding

We also demonstrate the teleported gate using a simple Fock encoding, with basis states \(\left|0\right\rangle \) and \(\left|1\right\rangle \), using the lowest two energy levels of the cavity to specify the data qubit. This basis is not a logical encoding according to our definition because it does not allow for quantum error correction; however, by specifying the data qubits in this basis, we can extract an upper bound for the performance of the teleported gate using our current device.

Teleported gate protocol

Before each experimental run, the entire system is initialized in the ground state by an active-feedback cooling sequence. An initial state is encoded onto the data qubits by using the communication qubits as an ancilla for the data qubits. We generate the initial state in the communication qubits and then apply an encoding optimal-control pulse that transfers this state onto the logical basis of the data qubits (Supplementary Information). We design this operation to return the communication qubit back to the ground state so it can be reused for the teleported gate sequence. We then perform the teleported CNOT gate. To analyse the resulting state, we perform tomography on the data qubits using one of two methods: by analysing the logical qubit state or by extracting the Wigner function. We provide a detailed pulse sequence of our experiment and a timing diagram in Extended Data Fig. 3.

In our experiment, it is important to track the reference frame of each data qubit, otherwise the local operations will fail. An important consequence of the Bell-state generation protocol is that the dispersive interaction induces a known, deterministic reference-frame shift on each of the data qubits; we account for this by updating the phase in subsequent steps of the teleported gate protocol. The communication-qubit measurements cause a conditional reference phase shift on the data qubits dependent on measurement outcome. Tracking these phases accurately is essential for all subsequent operations on the data qubits, and our controller dynamically updates the reference phase of all subsequent operations in real time. We provide further details on the measurement of these data-qubit reference phase shifts in Supplementary Information.

Data-qubit analysis

In the modular architecture, data qubits are designed to be well isolated from the environment and are therefore not measured directly. Instead, we repurpose the communication qubits and use them to measure the state of the data qubits. Using this indirect strategy we perform two types of measurement. In the first type of measurement, we measure the logical (or encoded) state of the data qubits. This is accomplished by first decoding the data-qubit state onto the communication qubit using an optimal-control decoding pulse and then measuring the desired observable on the communication qubit. Because the communication qubit is a transmon, we utilize standard techniques to enact rotations and single-qubit measurements to measure the logical observable. In the second type of measurement, we perform Wigner tomography to fully specify the cavity state36. We perform Wigner tomography using a Ramsey sequence on the communication qubit that maps the photon-number parity of the cavity state onto the state of the communication qubit.

Communication-qubit Bell-state generation

The Bell-state generation occurs while the data qubits store quantum information; the static dispersive interaction between the data and communication qubits, if not accounted for, will naturally entangle the data and communication qubits. Because it is necessary for the two qubits within each module to be disentangled at the end of this step, we modify our Bell-pair generation protocol and implement a refocused RIP sequence28 to echo away this unwanted interaction independently of the data-qubit encoding scheme (Extended Data Fig. 4a).

In our experiment, we utilize a RIP gate of length T = 300 ns, with pulse shape ε(t) = A{cos[πcos(πt/T)] + 1}, to minimize the residual photon population left in the bus cavity at the end of the pulse28. We achieve an entangling phase of ϕent = π in 672 ns and, combined with single communication-qubit rotations, create the Bell state \(| {\Psi }^{+}\rangle =(| ge\rangle +| eg\rangle )/\sqrt{2}\) with a state fidelity of 97% ± 1% (Extended Data Fig. 4b). To perform two-qubit tomography, we choose an over-complete set of 36 single-qubit rotations and use a maximum-likelihood estimate to reconstruct the density operator. We perform 10,000 averages for each tomography setting. Statistical errors are small in this experiment, around 0.2%, as extracted from a bootstrap analysis. Our uncertainty is estimated as the average of several experiments and roughly accounts for the run-to-run variations in our experiment.

Communication-qubit measurement and reset

The success of the teleported CNOT gate requires reliable measurements of each communication qubit. As discussed previously, our JPC-enabled single-qubit readout has assignment fidelities in excess of 99%. In our implementation of the teleported gate, the communication qubits serve dual roles: to store inter-module entanglement and to enable complex data-qubit operations via optimal-control pulses. Therefore, after the measurement of the communication qubits in our protocol, we perform a feedback reset of both communication qubits to the ground state to recycle them for the following single-qubit operations and tomography steps. These measurements are required to be highly quantum-non-demolition to the communication qubit and the data qubits.

We perform the following experiment to test the measurement and the reset. First, we initialize the two communication qubits in an equal superposition of computational states: \(| {\psi }_{{\rm{init}}}\rangle =(| gg\rangle +| ge\rangle +| eg\rangle +| ee\rangle )/2\). Next, we perform measurements on each qubit, allowing the controller to perform real-time state estimation. Conditioned on the measurement results, we apply a π-pulse if the qubit was measured to be in the excited state. Finally, we analyse the state via conditioned state tomography to assess the quality of the reset. The resulting tomograms are shown in Extended Data Fig. 5. We extract state infidelities to the joint ground state \(| gg\rangle \) of less than 1% for the case when we measured both qubits in the ground state (outcome ‘00’). We observe single-qubit infidelities of 2% and 4% when each qubit is measured to be in the excited state. The result from outcome ‘11’ indicates that these infidelities are additive and any crosstalk in the measurement or control is negligible. From these results, we find an average reset infidelity of about 3%, primarily limited by decay during the measurement and subsequent controller latency. From this experiment we establish that our system exhibits highly accurate and quantum-non-demolition single-qubit measurements.

Communication-qubit state tomography

For tomography on the two communication qubits, which are physically transmon qubits, it is convenient to decompose the state in the Pauli basis: \(\hat{\rho }={\sum }_{a}{p}_{a}{\hat{\sigma }}_{a}\), where \({\hat{\sigma }}_{a}\in {\{\hat{I},\hat{X},\hat{Y},\hat{Z}\}}^{\otimes 2}\) are the generalized Pauli operators. We then choose the overcomplete set of single-qubit rotations \({\{\hat{I},{\hat{R}}_{x}({\rm{\pi }}),{\hat{R}}_{x}(\pm {\rm{\pi }}/2),{\hat{R}}_{y}(\pm {\rm{\pi }}/2)\}}^{\otimes 2}\) as tomography operations. Experimentally, we perform independent \(\hat{Z}\)-measurements of each communication qubit, thus extracting two bits of information for each shot. Ideally, this generates the set of computational-state projection operators: \(\{{\hat{\Pi }}_{gg},{\hat{\Pi }}_{ge},{\hat{\Pi }}_{eg},{\hat{\Pi }}_{ee}\}\), where \(\left|{\hat{\Pi }}_{jk}\right\rangle =\left|jk\right\rangle \left\langle jk\right|\). In practice, we calibrate the measurement operators by preparing each of the four computational states and performing our two-bit measurement. The experimental positive-operator-valued measure elements \(\{{\hat{P}}_{jk}\}\) are then given as \({\hat{P}}_{jk}={\rm{diag}}[Pr( \mbox{`} 00\mbox{'}| \left|jk\right\rangle ),Pr( \mbox{`} 01\mbox{'}| \left|jk\right\rangle ),Pr( \mbox{`} 10\mbox{'}| \left|jk\right\rangle ),Pr( \mbox{`} 11\mbox{'}| \left|jk\right\rangle )]\); that is, we extract the probability of the four possible measurement outcomes when we prepare \(\left|jk\right\rangle \in \{\left|gg\right\rangle ,\left|ge\right\rangle ,\left|eg\right\rangle ,\left|ee\right\rangle \}\). This analysis assumes that the measurement operator is sensitive to only the \(\hat{Z}\) component of the qubit state, and from previous work in which quantum detector tomography was performed37, we find this to be a reasonable assumption.

Data-qubit state tomography

Reliable state tomography is predicated on ensuring small state preparation and measurement errors. However, when considering tomography on the data qubits (and in contrast to tomography on the communication qubits), it is no longer the case that we have a set of trusted operations to effect necessary operations and measurements on these multi-level systems. Therefore, we perform an indirect characterization29 of logical qubit operations \({\hat{U}}_{{\rm{op}}}\), whereby we perform tomography on the communication qubits for the composite operation \({\hat{U}}_{{\rm{dec}}}{\hat{U}}_{{\rm{op}}}{\hat{U}}_{{\rm{enc}}}\). The protocol begins and ends in the communication-qubit subspace and allows the use of trusted operations and measurements on the communication qubits. Then, by comparing this experiment to the case in which we perform the encoding and decoding pulses, \({\hat{U}}_{{\rm{dec}}}{\hat{U}}_{{\rm{enc}}}\), we isolate the performance of only \({\hat{U}}_{{\rm{op}}}\).

Process tomography

Our approach to performing logical process tomography on the teleported CNOT gate requires performing state tomography on a complete set of two-qubit initial states; here, we choose an overcomplete set of 36 input states \({\left\{\left|\pm {Z}_{{\rm{L}}}\right\rangle ,\left|\pm {X}_{{\rm{L}}}\right\rangle ,\left|\pm {Y}_{{\rm{L}}}\right\rangle \right\}}^{\otimes 2}\). Experimentally, we apply the appropriate rotation on each communication qubit and use optimal-control pulses to encode the state onto the data qubit. Then, we perform the teleported CNOT gate and subsequently apply a decoding optimal-control pulse to map the data-qubit states onto the communication qubits. With the quantum state contained in the communication qubit, we then perform state tomography on the communication qubits to reconstruct the state. With this set of ideal input states and experimentally reconstructed output states, we perform an inversion to extract the process that maps input states to output states. We represent the reconstructed process using the Pauli transfer matrix \({{\mathscr{R}}}_{{\rm{CNOT}}}\), which relates input Pin and output Pout states in the Pauli basis38, \({{\boldsymbol{P}}}_{{\rm{out}}}={{\mathscr{R}}}_{{\rm{CNOT}}}{{\boldsymbol{P}}}_{{\rm{in}}}\). In Extended Data Fig. 6, we present conditioned process tomography results with and without feedforward operations for the binomial encoding; equivalent results for the Fock encoding are provided in Supplementary Information. We perform a total of six pre- and post-rotations for quantum process tomography (QPT), leading to a total of 64 = 1,296 tomography settings. Each tomography setting consists of 2,500 averages. For each, the statistical error as extracted from a bootstrap analysis is less than 1%; error bars reported in the main text represent an estimate of the run-to-run variation, which is around 2%.

Figures of merit

In this work we use the following two measures for state and process fidelity: (1) the fidelity39 between two states ρ and σ,

$${{\mathscr{F}}}_{{\rm{state}}}(\rho ,\sigma )={\rm{tr}}{\left(\sqrt{{\rho }^{1/2}\sigma {\rho }^{1/2}}\right)}^{2}$$

and (2) the fidelity38 between two processes \({{\mathscr{R}}}_{1}\) and \({{\mathscr{R}}}_{2}\),

$${{\mathscr{F}}}_{{\rm{process}}}({{\mathscr{R}}}_{1},{{\mathscr{R}}}_{2})=\frac{{\rm{tr}}({{\mathscr{R}}}_{1}^{\top }{{\mathscr{R}}}_{2})/d+1}{d+1}$$

with d = 2n and n the number of qubits. We use the standard formula40 to calculate the concurrence \({\mathscr{C}}\).

The process fidelity calculated above is similar to the average gate fidelity, which for two processes \({{\mathscr{E}}}_{1}\) and \({{\mathscr{E}}}_{2}\) is generally defined as

$${{\mathscr{F}}}_{{\rm{avg}}}\equiv \int {{\mathscr{F}}}_{{\rm{state}}}[{{\mathscr{E}}}_{1}(\rho ),{{\mathscr{E}}}_{2}(\rho )]{\rm{d}}\psi $$