Quantum efficiency, purity and stability of a tunable, narrowband microwave single-photon source

Abstract

We demonstrate an on-demand source of microwave single photons with 71–99% intrinsic quantum efficiency. The source is narrowband (300 kHz) and tuneable over a 600 MHz range around 5.2 GHz. Such a device is an important element in numerous quantum technologies and applications. The device consists of a superconducting transmon qubit coupled to the open end of a transmission line. A π-pulse excites the qubit, which subsequently rapidly emits a single photon into the transmission line. A cancellation pulse then suppresses the reflected π-pulse by 33.5 dB, resulting in 0.005 photons leaking into the photon emission channel. We verify strong antibunching of the emitted photon field and determine its Wigner function. Non-radiative decay and 1/f flux noise both affect the quantum efficiency. We also study the device stability over time and identify uncorrelated discrete jumps of the pure dephasing rate at different qubit frequencies on a time scale of hours, which we attribute to independent two-level system defects in the device dielectrics, dispersively coupled to the qubit. Our single-photon source with only one input port is more compact and scalable compared to standard implementations.

Introduction

The single photon—the fundamental excitation of the electromagnetic field—plays a key role in quantum physics and can find practical application in quantum sensing¹, communication², and computing^3,4,5. Recently, considerable progress has been made in the generation of optical photons, e.g. by using quantum dots^6,7,8. However, in the microwave domain, the much smaller photon energy introduces many constrains for the realization of single-photon sources; for instance, operation at millikelvin temperatures is necessary to avoid thermal generation of photons. Narrowband microwave single photons are essential for precise interactions with circuits exhibiting a shaped energy structure, such as coplanar resonators⁹, three-dimensional cavities¹⁰, and acoustic-wave resonators^11,12, which can be used as quantum memories.

Superconducting quantum circuits are suitable for the implementation of on-demand microwave photon sources. So far, several different methods have been used. The first method is based on a qubit coupled to a resonator^13,14,15, where the source bandwidth is limited by the linewidth of the resonator. Secondly, in refs. ^16,17,18, single photons are generated due to inelastic Cooper-pair tunneling. This type of source has a high emission rate, but it cannot generate a superposition of vacuum and a single-photon Fock state. Thirdly, a single-photon generator based on emission from a qubit into a waveguide requires proper engineering of the asymmetric couplings to the control and emission channels^19,20,21,22. Finally, shaped single photons emitted from a qubit located near the end of a transmission line with a tunable-impedance termination²³ were demonstrated in experiment²⁴. None of these experiments included a thorough study of the photon leakage of the excitation pulse from the control to the emission channel, which affects the purity of the single-photon.

In this work, we implement a theoretical proposal from ref. ²³: a frequency-tunable qubit is capacitively coupled to the end of an open transmission line^25,26. Only a single channel exists in our system, so that the qubit, excited by a π-pulse, can only release a single photon back to the input. We cancel the π-pulse, after its interaction with the qubit, by interfering it with another, phase-shifted pulse and show a photon leakage 0.5% of a photon from the excitation pulse. The intrinsic quantum efficiency of our single-photon source is 71–99% over a tuneable frequency range of 600 MHz around 5.2 GHz, which is about 1600 times larger than the single-photon linewidth (300 kHz). This bandwidth is more than 20 times narrower than that of the tuneable microwave single-photon sources reported in refs. ^{16,17,18,20,21,22,24}.

Different from refs. ^16,17,18, our single-photon source allows to generate a superposition of vacuum and a single-photon Fock state. Moreover, compared to other results with more than one input ports^20,21,22,24, our single-port single-photon source does not require engineering of the asymmetric couplings on chip and is more compact and scalable as the number of sources increase.

Importantly, the intrinsic quantum efficiency—the fidelity only due to the emitter coherence—can be limited by both the pure dephasing rate and the non-radiative decay rate of the emitter. It is important to understand the noise mechanisms determining these rates in order to make further improvements. We systematically study the limitation of the intrinsic quantum efficiency and the temporal fluctuations of the single-photon source over 136 h. The result shows that both non-radiative decay and 1/f flux noise can affect the quantum efficiency from different types of two-level systems (TLSs). In addition, we also characterize the fluctuations of the pure dephasing rate due to dispersively coupled TLS defects with a narrow linewidth, which can lead to a decrease of the quantum efficiency by up to 60%.

Results

Experimental setup and procedure for single-photon emission

Our device consists of a magnetic-flux-tunable Xmon-type transmon qubit, capacitively coupled to the open end of a one-dimensional coplanar-waveguide transmission line. This zero-current boundary condition behaves as a mirror for the incoming microwave radiation. The corresponding simplified circuit diagram is shown in Fig. 1a. An asymmetric beam splitter, implemented by a 20 dB directional coupler, is connected to the sample to provide channels for qubit excitation and pulse cancellation. The circuit is made of aluminum on a silicon substrate, and is fabricated with a standard lithography process²⁷. The sample is characterized at T = 10 mK with its parameters shown in Table 1.

Fig. 1: Pulse cancellation.

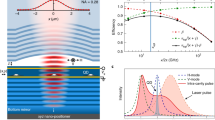
a Schematic for generating single photons using pulse cancellation. A flux-tunable transmon-type superconducting qubit (artificial atom) capacitively coupled to the end of an open transmission line with a −20 dB directional coupler connected to the transmission line. C_s and C_c represent the shunt capacitance for the qubit and the coupling capacitance between the qubit and the transmission line, respectively. Φ is the external magnetic flux threading the SQUID (Superconducting QUantum Interference Device) loop and JJ denotes the Josephson junctions. b Comparison of a π-pulse with and without the cancellation when the qubit is tuned away. The input pulse is suppressed by −33.5 dB with a cancellation pulse with 5.12 × 10⁵ averages. c Comparison between the canceled π-pulse from b and the photon emission by the qubit (red line) after a π/2-pulse with the pulse cancellation on. The red line is a fit to an exponential decay to extract Γ₂/(2π) = 193 ± 4 kHz.

Table 1 Device parameters.

As shown in Fig. 1a, we send a pulse to the input port of the directional coupler with the amplitude a_in(t)/A, where A = 0.1 is the attenuation from the −20 dB directional coupler. Then, a_in(t) is the corresponding amplitude of the pulse at the qubit. The output field at the qubit, using the standard input-output relation, is ${a}_{{{{{{\rm{out}}}}}}}^{{{{{{\rm{q}}}}}}}(t)={a}_{{{{{{\rm{in}}}}}}}(t)-i\sqrt{{{{\Gamma }}}_{{{{{{\rm{r}}}}}}}}{\sigma }_{-}(t)$^23,28, where σ₋(t) is the emission operator of the qubit. By adding another pulse β(t)/A to the cancellation port of the directional coupler, we have ${a}_{{{{{{\rm{out}}}}}}}(t)={a}_{{{{{{\rm{out}}}}}}}^{{{{{{\rm{q}}}}}}}(t)+\beta (t)$ at the output of the directional coupler. When β(t) = −a_in(t), we have ${a}_{{{{{{\rm{out}}}}}}}(t)=-i\sqrt{{{{\Gamma }}}_{{{{{{\rm{r}}}}}}}}{\sigma }_{-}(t)$ (the small red pulse). This means we obtain a single photon if a_in(t) is a π-pulse, and a superposition of vacuum and a single-photon Fock state if a_in(t) is a π/2-pulse.

We adjust the external flux to zero (Φ = 0) so that the qubit reaches its highest frequency ω₀₁. We then send a calibrated Gaussian pulse $\propto \exp (-{t}^{2}/2{\xi }^{2})$ with ξ = 20 ns which is on resonance with the qubit, so that it acts as a π-pulse. We measure the output field using a traveling-wave parametric amplifier (TWPA)²⁹ followed by a high electron mobility transistor amplifier (HEMT) (Fig. 7). Both quadratures of the signal output from the directional coupler, with and without the cancellation, are amplified and recorded by a digitizer (not shown) as a voltage V(t) = I(t) + iQ(t). The voltage is then normalized by the system gain from the on-resonance Mollow triplet^30,31,32. After averaging, the corresponding photon number at the qubit is defined as

$$n=\frac{1}{2{Z}_{0}\hslash {\omega }_{01}}\int\nolimits_{{t}_{0}}^{{t}_{1}}\left(| \langle V(t)\rangle {| }^{2}-| \langle {V}_{N}\rangle {| }^{2}\right)\ {{{{{\rm{d}}}}}}t$$

(1)

where t₀ and t₁ denote when the signal starts and ends, respectively. Note that for the qubit emission, t₀ is the time corresponding to the maximal amplitude of the emission. 〈V_N〉 is the averaged system voltage noise and Z₀ ≈ 50 Ω is the waveguide impedance.

Figure 1b shows the power of the input π-pulse as a function of time. The black line indicates the power of the input pulse at the sample after the gain calibration when the qubit is tuned away, while the blue one corresponds to the residual pulse after cancellation. The result shows a 33.5 dB suppression of a π-pulse in power due to the cancellation, resulting in a photon leakage of ${n}_{{{{{{\rm{leak}}}}}}}^{{{{{{\rm{meas}}}}}}}=0.0049$, according to Eq. (1). In Fig. 1c, we also measure the coherent emission (red line) from the qubit decay after a π/2-pulse and fit the data to an exponential curve (black) with a decay rate Γ₂/(2π) = 193 ± 4 kHz. By taking the integral over time with Eq. (1) starting from t₀ = 252 ns, we obtain the photon numbers ${n}_{{{{{{\rm{q}}}}}}}^{{{{{{\rm{meas}}}}}}}\approx 0.173$ for the qubit emission. This agrees well with the formula Γ_r/8Γ₂ = 0.1795 derived below. We notice that ${n}_{{{{{{\rm{q}}}}}}}^{{{{{{\rm{meas}}}}}}}$ is less than 0.5 since we just measure the coherent part of the qubit emission.

The leakage from the excitation pulse can also be estimated without calibrating the system gain as follows. The driven qubit generates a voltage amplitude of V_q(t) = i2ω₀₁Z₀C_cdσ₋(t)²⁰, where d is the qubit dipole moment, and C_c represents the coupling capacitance between the qubit and the transmission line. The radiative decay rate is given by ${{{\Gamma }}}_{{{{{{\rm{r}}}}}}}={S}_{{{{{{\rm{v}}}}}}}(\omega ){({C}_{{{{{{\rm{c}}}}}}}d)}^{2}/{\hslash }^{2}$ with S_v(ω) = 2$\hslash$ ω₀₁Z₀ being the spectral density of the voltage quantum noise in the transmission line where we ignore the effect from the thermal noise inside the waveguide since $\hslash$ω₀₁ ≫ k_BT. Therefore, the corresponding emission power from the qubit is $| {V}_{{{{{{\rm{q}}}}}}}(t){| }^{2}/(2{Z}_{0})=\hslash {\omega }_{01}{{{\Gamma }}}_{{{{{{\rm{r}}}}}}}| {\sigma }_{-}(0){| }^{2}{e}^{-2{{{\Gamma }}}_{2}t}$ where we have ${\sigma }_{-}(t)={\sigma }_{-}(0){e}^{-{{{\Gamma }}}_{2}t}$. By taking the integral over time, the photon number is n_q = Γ_r/(2Γ₂)∣σ₋(0)∣² = Γ_r/8Γ₂. Combining the values of Γ_r and Γ₂ in Table 1, the leakage from the π-pulse is ${n}_{{{{{{\rm{leak}}}}}}}={n}_{{{{{{\rm{leak}}}}}}}^{{{{{{\rm{meas}}}}}}}/{n}_{{{{{{\rm{q}}}}}}}^{{{{{{\rm{meas}}}}}}}\times {n}_{{{{{{\rm{q}}}}}}}\approx 0.005$. In reality, ∣σ₋(0)∣ < 0.5 due to the small emission during a π/2-pulse. Here, we ignore this since our pulse length is much shorter than the qubit lifetime. We emphasize that the amplitude of the canceled pulse in Fig. 1b, c was minimized by adjusting the amplitude of the cancellation pulse, the phase difference between the input and the cancellation pulse and compensating the time delay between these two pulses. Compared to directly measuring the qubit emission power after a π-pulse, we take an advantage of the coherent emission after a π/2-pulse so that the system noise can be averaged out with much fewer averages.

Qubit operation

Next we vary the pulse length τ, and measure the integral of free-decay traces such as the one in Fig. 1c, normalized to the number of points in the trace. In order to maximize the signal, we digitally rotate the integrated value into the I quadrature. Meanwhile, we also record the second moment of the emitted field which corresponds to the emitted power 〈P〉 = 〈(I² + Q²)〉. Figure 2 shows the Rabi oscillations of 〈I〉 and 〈P〉 with pulse lengths up to 1.4 μs. The signal is averaged over 1.28 * 10⁴ repetitions. The background offset from the system noise is removed from each data point of the power oscillation. The clear oscillatory pattern in the figure is a manifestation of the coherence of photons emitted by the qubit. By solving the Bloch equations we obtain

$$\begin{array}{l}\langle {\sigma }_{y}\rangle =\frac{{{\Omega }}}{{{{\Omega }}}^{2}+{{{\Gamma }}}_{1}{{{\Gamma }}}_{2}}[{{{\Gamma }}}_{1}+{e}^{-{{{\Gamma }}}_{{{{{{\rm{s}}}}}}}\tau }\sqrt{{{{\Gamma }}}_{1}^{2}+{B}_{1}^{2}}\sin ({{{\Omega }}}_{{{{{{\rm{m}}}}}}}\tau -{\theta }_{1})]\\ \langle {\sigma }_{z}\rangle =\frac{-{{{\Gamma }}}_{1}{{{\Gamma }}}_{2}-{{{\Omega }}}^{2}{e}^{-{{{\Gamma }}}_{{{{{{\rm{s}}}}}}}\tau }\sqrt{1+{B}_{2}^{2}}\sin ({{{\Omega }}}_{{{{{{\rm{m}}}}}}}\tau +{\theta }_{2})}{{{{\Omega }}}^{2}+{{{\Gamma }}}_{1}{{{\Gamma }}}_{2}},\end{array}$$

(2)

where Γ₁ is the relaxation rate of the qubit and Ω is the Rabi frequency, Γ_s = (Γ₁ + Γ₂)/2, ${{{\Omega }}}_{{{{{{\rm{m}}}}}}}=\sqrt{{{{\Omega }}}^{2}-{({{{\Gamma }}}_{1}-{{{\Gamma }}}_{2})}^{2}/4}$, ${B}_{1}={{{\Omega }}}_{{{{{{\rm{m}}}}}}}-({{{\Gamma }}}_{1}^{2}-{{{\Gamma }}}_{2}^{2})/(4{{{\Omega }}}_{{{{{{\rm{m}}}}}}})$, ${B}_{2}={{{\Gamma }}}_{{{{{{\rm{s}}}}}}}/{{{\Omega }}}_{{{{{{\rm{m}}}}}}}=\cot {\theta }_{2}$ and ${{{\Gamma }}}_{1}/{{{\Omega }}}_{{{{{{\rm{m}}}}}}}\approx \tan {\theta }_{1}$. Since 〈I〉 ∝ 〈σ_y〉 and 〈P〉 ∝ 1 + 〈σ_z〉, we take Eq. (2) to fit the data to obtain Γ_s/2π = 316 ± 6 kHz and θ₂ + θ₁ = (0.498 ± 0.004)π. The phase difference indicates that the measured radiation is not from a coherent state in which the power and amplitude would oscillate in phase.

Fig. 2: Quadrature and power oscillations of emitted radiation from the driven qubit vs pulse length τ.

Red stars represent the measured I quadrature amplitude, while blue stars correspond to the emitted power 〈P〉 = 〈(I² + Q²)〉. Both traces are fitted to a sinusoid function with an exponential-decay envelope, simultaneously. The extracted decay rate is 2π * 629 kHz. Moreover, the phase of the two fitting curves is offset by π/2, which rules out a coherent state and provides evidence for single-photon emission. The top axis indicates the angle of the qubit-state rotation on the Bloch sphere. The external flux is Φ = 0.

To demonstrate that our device indeed is a single-photon source we extract the second-order correlation function g⁽²⁾(0) and we reconstruct the Wigner function W(α)³³. We send either a π-pulse or a π/2-pulse to excite the qubit. With an appropriate mode-matching filter with an exponential decay, we obtain the quadrature histograms of the measured single-shot voltages normalized by the gain value. The single-shot measurement is repeated up to 2.56 * 10⁷ times. By then subtracting the reference values measured in the absence of the pulse, as outlined for example in ref. ³⁴, we extract the moments of the photon mode a. Figure 3a shows the moments ∣〈a〉∣, 〈a^†a〉 and $\langle {({a}^{{{\dagger}} })}^{2}{a}^{2}\rangle$ of the qubit emission after a π-pulse and a π/2-pulse, respectively. The first and second-order moments are 0.036 ± 0.001 and 0.618 ± 0.003 for a π-pulse, and 0.399 ± 0.035 and 0.337 ± 0.002 for a π/2-pulse. The second order of moments shows that the overall quantum efficiencies at the maximum qubit frequency are 61.8% for a single-Fock state $\left|1\right\rangle$ after a π-pulse, and 67.4% for a superposition state $(\left|0\right\rangle +\left|1\right\rangle )/\sqrt{2}$ after a π/2-pulse. In our case, the maximum photon number is just one so that we only need to consider up to the fourth order of the moments corresponding to two photons.

Fig. 3: Moments and Wigner functions.

a The bar chart with error bars for two standard deviations shows a comparison between the experiment (red) and theory (white) for the moments of a single-photon state $\left|1\right\rangle$ after a π-pulse pulse and a superposition state $(\left|0\right\rangle +\left|1\right\rangle )/\sqrt{2}$ after a π/2-pulse. b Wigner functions corresponding to the moments obtained from the experiment in (a) using a maximum likelihood method^34,36.

The moments we extract differ from the theoretically expected 〈a^†a〉 = 1 for the Fock state and ∣〈a〉∣ = 0.5 for the superposition state. The numerical result from simulating the dynamics of the qubit by using QuTip³⁵ shows that the population of the first excited level of our qubit is given by the density matrix element ρ₁₁ = 0.93 after a π-pulse with ξ = 20 ns, and ∣σ₋∣ = 0.44 after a π/2-pulse with ξ = 20 ns. The normalized filter for the mode matching is $f(t)=\sqrt{{{{\Gamma }}}_{1}}{e}^{-{{{\Gamma }}}_{1}/2t}$, leading to 〈a^†a〉 = Γ_r/Γ₁ and $| \langle a\rangle | =2\sqrt{{{{\Gamma }}}_{{{{{{\rm{r}}}}}}}{{{\Gamma }}}_{1}}/(2{{{\Gamma }}}_{2}+{{{\Gamma }}}_{1})$. In summary, we have 〈a^†a〉 = 0.93*Γ_r/Γ₁ and $\langle a\rangle =0.44* 2\sqrt{{{{\Gamma }}}_{{{{{{\rm{r}}}}}}}{{{\Gamma }}}_{1}}/(2{{{\Gamma }}}_{2}+{{{\Gamma }}}_{1})$. Combining the decay rates in Table 1 and assuming that the pure dephasing rate is zero (Fig. 4b) at the maximum qubit frequency (Φ = 0), we get 〈a^†a〉 = 0.67 and ∣〈a〉∣ = 0.36, which are close to our measured results. From this discussion, we can conclude that the non-radiative decay is the main factor that limits the quantum efficiency of our single-photon source at the flux sweet spot, and the overall quantum efficiency are limited by both the imperfect qubit excitation and the qubit coherence.

Fig. 4: Intrinsic quantum efficiency, pure dephasing and non-radiative decay rates as a function of the qubit frequency.

a The intrinsic quantum efficiency η_q for our single-photon source over the 600 MHz tunable range. The efficiency is limited by the pure dephasing rate and the non-radiative decay rate of the qubit. These two factors reduce the efficiency by η_p and η_n respectively, where we have η_q + η_p + η_n = 1. b Pure dephasing rate Γ_ϕ as a function of the qubit frequency. c Nonradiative decay rate Γ_n as a function of the qubit frequency, where we have ${{{\Gamma }}}_{{{{{{\rm{n}}}}}}}^{{{{{{\rm{Decay}}}}}}}={{{\Gamma }}}_{{{{{{\rm{1}}}}}}}^{{{{{{\rm{Decay}}}}}}}-{{{\Gamma }}}_{{{{{{\rm{r}}}}}}}$ and ${{{\Gamma }}}_{{{{{{\rm{n}}}}}}}^{{{{{{\rm{M.T.}}}}}}}={{{\Gamma }}}_{{{{{{\rm{1}}}}}}}^{{{{{{\rm{M.T.}}}}}}}-{{{\Gamma }}}_{{{{{{\rm{r}}}}}}}$. ${{{\Gamma }}}_{{{{{{\rm{1}}}}}}}^{{{{{{\rm{Decay}}}}}}}$ and ${{{\Gamma }}}_{{{{{{\rm{1}}}}}}}^{{{{{{\rm{M.T.}}}}}}}$ are extracted from the exponential decay of the qubit power emission and the off-resonant Mollow-triplet spectrum from the qubit fluorescence, respectively. The value of Γ_r is from the reflection coefficient measurement. In all panels, the error bars are two standard deviations.

Of particular interest is the normalized zero-time-delay intensity correlation function ${g}^{(2)}(0)=\langle {({a}^{{{\dagger}} })}^{2}{a}^{2}\rangle /{\langle {a}^{{{\dagger}} }a\rangle }^{2}$. Its values of 0 ± 0.0139 and 0 ± 0.0264 for π and π/2-pulses show an almost complete antibunching of the microwave field, demonstrating that the output is almost purely a single photon. To further demonstrate that our source is nonclassical, in Fig. 3b, we reconstruct the Wigner function from the relation $W(\alpha )=(2/\pi ){{{{{\rm{Tr}}}}}}[\hat{D}(\alpha )\rho {\hat{D}}^{{{\dagger}} }(\alpha )\hat{{{\Pi }}}]$, by using a maximum likelihood method^34,36, where $\hat{D}(\alpha )$ is the displacement operator with a coherent state α, $\hat{{{\Pi }}}$ is the parity operator and ρ is the extracted density matrix of the filtered output from the different orders of moments.

Besides the photon leakage, there are a number of different properties that are important for proper operation of the single-photon source, such as frequency tunability, quantum efficiency, stability, bandwidth and repetition rate. In the following paragraphs we study and evaluate these quantities for our single-photon source.

Bandwidth, repetition rate, and tunability

The repetition rate for our source is limited by the coupling strength between the qubit and the transmission line which can be varied over a wide range by design. For our sample the relaxation rate at the sweet spot is ~2π × 376 kHz, resulting in a repetition time of about 2.5 μs where the time is several times longer than the qubit lifetime T₁ = 1/Γ₁ ≈ 420 ns.

Our single-photon source is frequency-tunable over a wide frequency range. The operation frequency is adjusted by changing the qubit frequency with the external magnetic flux and adjusting the frequency of the microwave source that generates the π-pulse and the cancellation pulse. Here we show tunability of up to 600 MHz, where it is limited by flux noise producing large jumps in the qubit frequency when the qubit is tuned too far away from the flux sweet spot (Φ = 0).

Intrinsic quantum efficiency

Different from the overall quantum efficiency, the intrinsic quantum efficiency only depends on the qubit coherence, which is the upper bound for the overall efficiency. We also investigate the intrinsic quantum efficiency which is given by η_q = Γ_r/(2Γ₂), of our single-photon source over the frequency range 4.9–5.5 GHz. The quantum efficiency is in the range 71–99% (red in Fig. 4a), extracted from the reflection coefficient. Typically, the pure dephasing rate Γ_ϕ can decohere the supposition of vacuum and a single-photon Fock state, resulting in a decrease in the single-photon quantum efficiency. Moreover, a single photon can be dissipated into the environment through the non-radiative decay channel due to the qubit interaction with the environment. We denote that the reduction of the quantum efficiency from these two effects as η_p = Γ_ϕ/Γ₂ and η_n = Γ_n/2Γ₂, respectively. Here, the values of η_p are based on the exponential decay from the qubit emission as discussed below (black, in Fig. 4a). Then, we calculate η_n indirectly, from η_n = Γ_n/2Γ₂ = 1 − η_p − η_q (blue, in Fig. 4a). we find that the non-radiative decay only affects the quantum efficiency near the maximal qubit frequency. When we tune the qubit frequency down, the pure phasing dominates the reduction of the quantum efficiency. Therefore, it is necessary to understand which type of noise induces the pure dephasing rate.

To extract Γ_ϕ, we send a pulse with the amplitude close to a π/2-pulse, and measure the qubit emission with 3.84 × 10⁷ averages. From the emission decay, we can extract both Γ₁ and Γ₂, the power decay $\propto {e}^{-{{{\Gamma }}}_{{{{{{\rm{1}}}}}}}t}$, and the quadrature decay $\propto {e}^{-{{{\Gamma }}}_{{{{{{\rm{2}}}}}}}t}$. Then, Γ_ϕ can be calculated from Γ_ϕ = Γ₂ − Γ₁/2. In Fig. 4b, the data (black) shows that the pure dephasing rate increases when the qubit is tuned away from the flux sweet spot further. The averaged pure dephasing rate $\overline{{{{\Gamma }}}_{\phi }}$ over the whole frequency range is about 2π*10 Hz. The pure dephasing rate Γ_ϕ due to 1/f flux noise with the flux noise spectral density S_Φ(f) = A_Φ/f has the relationship ${{{\Gamma }}}_{\phi }=\sqrt{{A}_{{{\Phi }}}| {{{{\mathrm{ln}}}}}\,(2\pi {f}_{{{{{{\rm{IR}}}}}}}t)| }\frac{\partial {\omega }_{01}}{\partial {{\Phi }}}$³⁷. f_IR is the infrared cutoff frequency, taken to be 5 mHz determined by the measurement time, and t is on the order of ${\overline{{{{\Gamma }}}_{\phi }}}^{-1}$. Using this relationship to fit the extracted Γ_ϕ values shown as a dashed line in Fig. 4b, we obtain ${A}_{{{\Phi }}}^{1/2}\approx 2\mu {{{\Phi }}}_{0}$, which is consistent with other measurements^37,38.

In Fig. 4c, from 5.51 to 5.39 GHz, we find that the non-radiative decay rate Γ_n decreases gradually from 100 kHz to zero. We suspect that some TLSs with a certain bandwidth are located around the flux sweet spot. Since in this range the pure dephasing rate Γ_ϕ is less than 20 kHz (Fig. 4b) with the increasing rate slower than the reduction rate of Γ_n, the quantum efficiency of our single-photon source in Fig. 4a grows from 80 to 94%. Especially near the flux sweet spot, the non-radiative decay is several times larger than the pure dephasing rate, leading to the quantum efficiency mainly limited by the non-radiative decay. At the two exceptional data points where we obtain negative values of Γ_n (Fig. 4c), around 5.2 GHz, the efficiency is up to 99%, indicating that during the reflection coefficient measurement at this frequency, both the pure dephasing rate and non-radiative decay rate are very small. When we tune the qubit frequency further away from the flux sweet spot, the non-radiative decay remains close to zero whereas the pure decay rate is increased to be around 35 kHz, leading to a decreased quantum efficiency around 71%. (See a more detailed analysis in the “Methods” section).

Stability

Recently, many works demonstrated that fluctuating TLSs can limit the coherence of superconducting qubits^27,39,40,41. Here, we investigate how the fluctuations affect different properties of our single-photon source. We repeatedly measure Γ₁ and Γ₂ interleaved at Φ = 0 and Φ = 0.09Φ₀, corresponding to ω_01,1 = ω₀₁(0) = 2π × 5.51 GHz and ω_01,2 = ω₀₁(0.09Φ₀) = 2π × 5.39 GHz, respectively. At the same time, the fluctuations of the qubit frequency are also obtained from the phase information of the emitted field which carries information about the qubit operator $\langle {\sigma }_{-}\rangle \propto {e}^{i\delta {\omega }_{01}t}$ where δω₀₁ is the frequency difference between the frequency of the driving pulse and the qubit frequency. The total measurement spans 4.90 × 10⁵ s (~136 h) with 2000 repetitions for each qubit frequency. Each repetition has 3.20 × 10⁶ averages. From the values of Γ₁ and Γ₂, we extract Γ_ϕ values shown in Fig. 5a, b from averaging over 8 repetitions. We find that Γ₁ remains stable for both zero detuning and 120 MHz detuning in Fig. 6. By assuming that Γ_r is stable over time, this implies that for this detuning Γ_n is also stable on the scale of Γ_r.

Fig. 5: Fluctuations of the pure dephasing rate, the qubit frequency, and the quantum-efficiency reduction of the single-photon source.

a, b Fluctuations on the pure dephasing rate Γ_ϕ and the qubit frequency around ω_01,1/(2π) = 5.51 GHz and ω_01,2/(2π) = 5.39 GHz, corresponding to 0 and 120 MHz detunings, over 136 h. c Fluctuations of the reduction of the quantum efficiency, η_p, due to the fluctuations of Γ_ϕ at 0 MHz and 120 MHz detunings, over 136 h. In all panels, the error bars are two standard deviations.

Fig. 6: Fluctuations of the qubit frequency and decay rates.

a Fluctuations on the decay rates and the qubit frequency at ω_01,1/(2π) = 5.51 GHz, over 136 h. b Fluctuations on the decay rates and the qubit frequency at ω_01,2/(2π) = 5.39 GHz, over 136 h. In both panels, the error bars are two standard deviations.

However, the fluctuations of the qubit frequency, δ_f,i = (ω_01,i − 〈ω_01,i〉)/2π and the pure dephasing rate are obvious as shown in Fig. 5a for δ_f,1 and (b) for δ_f,2. First, we note the frequency jumps for the case of 120 MHz detuning (i.e. around ω_01,2) at t = 16 h and t = 90 h do not affect the pure dephasing rate. We suspect that this is due to a change in the flux offset through the SQUID, as we tune the qubit back and forth by the applied external flux that could induce a change in magnetic polarization in cold components. Therefore, we can not see significant fluctuations at the flux sweet spot.

Other frequency-switching events happening at t = 95 h and t = 120 h for 0 MHz detuning (i.e. around ω_01,1) and those before t = 10 h and at t = 64 h for 120 MHz detuning show a strong positive correlation with the pure dephasing rate. Interestingly, the fluctuations do not happen at the same time for both detunings. Combining this with the fact that Γ₁ is stable, we speculate that this is due to two uncorrelated TLSs with a small decay rate γ_i (i = 1, 2), close to ω_01,i, dispersively coupled to the qubit (see more details in the section “Methods”). Thus, these two TLSs can only cause the pure dephasing, but not dominate the relaxation, which can explain the stronger fluctuations in Γ_ϕ compared to Γ₁ shown in Fig. 6.

Evidently, these two TLSs reduce the intrinsic quantum efficiency substantially by up to 40% and 60% as shown in Fig. 5c for detunings of 0 and 120 MHz, respectively. The effect from TLSs is stronger than other types of noises, especially in the case of zero detuning. At zero detuning we also note that between these large fluctuations the single-photon source can be stable for tens of hours. However, the qubit becomes more sensitive to the 1/f flux noise when it is detuned by 120 MHz, it results in about a 20% fluctuation of the quantum efficiency over the total measurement time. This indicates that 1/f flux noise will be the dominant noise when we tune the qubit frequency away from the flux sweet spot.

Since our single-photon source has a narrow bandwidth it will be meaningful to investigate the frequency stability over a long time, from Fig. 5a, b, we find that at Φ = 0 the frequency fluctuations due to TLSs can be up to 100 kHz which is nearly one third of the single-photon linewidth (Γ_r = 270 kHz). However, just tuned down the qubit frequency by 120 MHz (Φ = 0.09), the external flux jumps described above dominate the frequency shift of the single-photon source, the shifts can be up to 200 kHz which is a factor of two compared to the effect from TLSs.

Discussion

In this paper, we demonstrate a method to implement a frequency-tunable single-photon source by using a superconducting qubit. We measure the moments of the emitted field, and from those we can evaluate both the second order correlation function and the Wigner function. Our study illustrates that the intrinsic quantum efficiency of our single-photon source can reach up to 99%, which could be improved further by engineering a large radiative decay rate of the qubit into the waveguide transmission line. Moreover, the photon leakage from the canceled input π-pulse is as low as 0.5% of a photon, indicating that our single-photon source is very pure. The frequency tunable range of our single-photon source corresponds to 1600 × Γ₁, reaching state of the art and enabling us to address quantum memories with a large number of different ‘colors.’

We also study the noise mechanisms which limit the intrinsic quantum efficiency in detail. The non-radiative decay rate and the pure dephasing rate from the 1/f flux noise both contribute to the reduced quantum efficiency. The 1/f flux noise could be decreased by reducing the density of surface spins by surface treatment of the sample, e.g. annealing⁴² and UV illumination⁴³.

Finally, we investigate the stability of our single-photon source, which is important for long time operation. The instability originates mainly from the increased sensitivity to 1/f flux noise when the source frequency is tuned down from the flux-insensitive bias point. The results show that the source can be stable for tens of hours at the maximum frequency. However, sometimes, the quantum efficiency decreases by up to 60% when the qubit couples to TLSs. Besides reducing the quantum efficiency, the TLSs can also change the frequency of the single photons by up to one third of the linewidth. However, the environment flux jump will be the dominant noise to shift the single-photon frequency, which could be further reduced by magnetic shields e.g. Cryoperm shielding^27,44.

Methods

Measurement setup and qubit characterization

Figure 7a shows the detailed experimental setup. To characterize the qubit a vector network analyzer (VNA) generates a weak coherent probe with the frequency ω_pr. The signal is fed into the input line, attenuated to be weak (Ω < Γ₁) and interacts with the qubit. Then, the VNA receives the reflected signal from the output line after the amplification to determine the complex reflection coefficient, r. Two-tone spectroscopy is then done to obtain the qubit anharmonicity. Specifically, we apply a strong pump at ω₀₁ to saturate the $\left|0\right\rangle -\left|1\right\rangle$ transition. Meanwhile, we combine a weak probe with the strong pump together via a 20 dB directional coupler. The frequency of the weak probe from the VNA is swept near the $\left|1\right\rangle -\left|2\right\rangle$ transition. When the probe is on resonance, again, we will get a dip in the magnitude response of r, leading to α = (ω₀₁ − ω₁₂)/$\hslash$ = 2π*0.251 GHz (not shown).

Fig. 7: The measurement setup.

LP, Iso, HEMT, and TWPA denote low-pass filters, isolators, a high electron mobility transistor amplifier, a traveling-wave parametric amplifier.

Fano-shape spectroscopy

When we measure the reflection coefficient at different qubit frequencies, we notice that at some frequencies the amplitude of the spectroscopy is not flat but has a Fano shape (Fig. 8a). This Fano shape may affect the extracted Γ_r values, and we argue that the Fano shape originates from an impedance mismatch in the measurement setup which will result in a modified reflection coefficient as³¹:

$$r=1-\frac{i{{{\Gamma }}}_{{{{{{\rm{r}}}}}}}{e}^{i\phi }}{{{\Delta }}+i{{{\Gamma }}}_{2}},$$

(3)

where

$$\tan (\phi )=\frac{{r}_{1}\sin 2{\phi }_{0}}{{t}_{1}^{2}{\beta }^{2}+{r}_{1}\cos 2{\phi }_{0}},$$

(4)

r₁ (t₁) is the reflection (transmission) coefficient at the place where the impedance mismatch is located, and β is proportional to the attenuation between the place and the sample. ϕ₀ = ωτ is the extra phase of the propagating wave from the propagating time τ, due to the distance between the qubit and the impedance mismatch. We use Eq. (3) to fit the data to extract the values of Φ at different qubit frequencies which are thus fit to Eq. (4) as show in Fig. 9a. The extracted r₁ ≈ 0.14 close to 0.1 (corresponding −20 dB in power) and β ≈ 0.97 corresponding to 0.26 dB attenuation indicate that the impedance mismatch probably arises from the directional coupler.

Fig. 8: Impedance mismatch.

Panels a, b are the magnitude and phase response of the reflection coefficient before compensating the impedance mismatch. Panels c, d are the magnitude and phase response of the reflection coefficient after compensating the impedance mismatch.

Fig. 9: Compensating the Fano-shape reflection coefficient.

a The phase ϕ in Eq. (4) vs. different qubit frequencies. Blue dots are the data with the solid curve as a fit. b, c The comparison of Γ₂ and Γ_r before and after compensating the impedance mismatch.

Afterwards, to compensate the impedance mismatch, we calculate r_comp = 1 − (1 − r_raw) * e^iϕ where r_raw is the raw data (blue in Fig. 8a, b). The magnitude response of r_comp in Fig. 8c manifests that the impedance mismatch has been corrected. We repeat this process for other qubit frequencies and then fit the calculated data to obtain Γ_r and Γ₂ (red stars in Fig. 9b, c). Comparing to the values before correcting the impedance mismatch (blue dots in Fig. 9b, c), we find they are close to each other.

Two-level fluctuator model

Figure 6 shows the fluctuations of Γ₁ and Γ₂ at ω_01,1/(2π) = 5.51 GHz and ω_01,2/(2π)5.39 GHz over 136 h. We denote g_i and Δ_i = (ω_TLS,i − ω_01,i)/(2π) as the coupling strength and the frequency detuning between the TLS and the qubit, respectively. In addition, Γ_n,i and Γ_1,i are the corresponding non-radiative decay rate and relaxation at each qubit frequency. To simplify the model, we let g₁ = g₂. When g_i ≪ Δ_i ≪ 120 MHz, we have a dispersive shift ${\chi }_{{{{{{\rm{i}}}}}}}={g}_{{{{{{\rm{i}}}}}}}^{2}/{{{\Delta }}}_{{{{{{\rm{i}}}}}}}$. Typically, the surface TLS coupling rates are on the order of g ≈ 100 kHz⁴⁰. Since the measured frequency shifts of both qubit frequencies are almost the same, about 40 kHz, the detuning to such a TLS is ~${{{\Delta }}}_{{{{{{\rm{i}}}}}}}={g}_{{{{{{\rm{i}}}}}}}^{2}/{\chi }_{{{{{{\rm{i}}}}}}}=2.5\,{{{{{\rm{MHz}}}}}}$, which is about 9 × Γ_1,i. From the shortest duration of the TLS fluctuations in Fig. 5b, we can estimate the switching time of these two TLSs roughly to be 2.88 × 10⁴ s and 7.82 × 10³ s, corresponding to γ₁ = 34.7 μHz and γ₂ = 127.9 μHz, respectively. According to ${{{\Gamma }}}_{{{{{{\rm{n}}}}}},{{{{{\rm{i}}}}}}}\propto {g}_{{{{{{\rm{i}}}}}}}^{2}/{{{\Delta }}}_{{{{{{\rm{i}}}}}}}^{2}{\gamma }_{{{{{{\rm{i}}}}}}}=0.16 \% {\gamma }_{{{{{{\rm{i}}}}}}}$. Thus, these two TLSs can only cause the pure dephasing, but not dominate the relaxation. This can also explain the stronger fluctuations in Γ_ϕ compared to Γ₁ shown in Fig. 6. We emphasize that the fresh finding here is that we notice TLSs can be activated independently where there is only a single TLS was investigated in ref. ⁴⁰.

Directional coupler parameters

Directional coupler parameters are shown in Table 2. The approximate values of the commercial directional coupler used in our setup as measured by a VNA. Even though these values are measured at room temperature, they should be close to the values at 10 mK. The attenuation between the input and a_in is about −21.7 dB including the insertion loss, very close to −20 dB which is the value printed on the coupler.

Table 2 Parameters for the directional coupler.

Measurement consistency

In order to obtain the non-radiative decay rate and the quantum-efficiency reduction from that, we need to combine results from different measurements as we discussed in Fig. 4. We obtain Γ_n = Γ₁ − Γ_r where Γ₁ can be either measured from the exponential decay of the qubit emission or the power spectrum, and Γ_r is based on the reflection coefficient. Therefore, it is necessary to check whether the qubit is stable over these measurements. In Fig. 10, we show the extracted values of Γ₂ from different methods, over the frequency range of 4.91–5.51 GHz. We find that the values of Γ₂ from different methods agree well except for the data points at 5.2 and 5.3 GHz. This inconsistency is probably due to the redistribution of TLSs^27,39 between different measurements, since there are a few-days delay when we take these different measurements. Because of this inconsistency, we have slightly negative values of Γ_n and η_n as shown in Fig. 4a, c, respectively.

Fig. 10: Comparison the values of Γ₂ extracted from different methods.

${{{\Gamma }}}_{{{{{{\rm{2}}}}}}}^{{{{{{\rm{Ref}}}}}}}$, ${{{\Gamma }}}_{{{{{{\rm{2}}}}}}}^{{{{{{\rm{M.T.}}}}}}}$ and ${{{\Gamma }}}_{{{{{{\rm{2}}}}}}}^{{{{{{\rm{Decay}}}}}}}$ are extracted from the reflection coefficient, off-resonant Mollow-triplet power spectrum and the exponential decay of the qubit emission after a π/2-pulse, respectively. In the plot, the error bars are for two standard deviations. Note that the slight difference at 5.1 GHz between the Mollow-triplet and other two measurements is from that the sampling rate of the digitizer is not large enough, leading to the truncation at the edge of the measured power spectrum. See more detail about how to use the power spectrum to extract the qubit decay rates in ref. ³⁰. The error bars are two standard deviations.