Introduction

Multistability in driven-dissipative models usually means the presence of two possible stationary states of the system that can be distinguished by local observable measurements. Although on the level of the mean-field approximation or for classical systems it can be easily established whether or not it exists1,2, its actual existence, in particular in low-dimensional strongly interacting systems remains quite controversial with both theoretical and experimental works reporting differing conclusions3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26. The existing approaches usually rely on sophisticated theoretical techniques for including perturbations of finite-size corrections to the mean-field or large scale efficient numerical simulations such as t-DMRG10 or projected entangled pair states (PEPS)21. The general lore in the literature is that the lower dimension, the more likely it is that the full quantum fluctuations (finite-system size corrections) will destroy the multistability and restore the generic unique stationary state of the model27,28,29,30. However, in general, the question remains unsettled in any dimension (see e.g., ref. 21 for an advanced numerical study in two dimensions). Therefore, exact results on this controversial problem are desirable.

There are two recently introduced concepts, dissipative time crystals31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46, which are systems that have persistent oscillations induced by the dissipation, and boundary time crystals47,48,49,50,51, which have persistent oscillations in the thermodynamic limit, only (cf. discrete, driven versions of time crystals under dissipation52,53,54,55,56,57,58 and other non-stationary phenomena beyond observables59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74). As the oscillations in our model are persistent in the thermodynamic limit, the model can be understood as a boundary time pseudo-crystal, with pseudo- implying that the oscillations amplitude decays with the system size for initial states with low entanglement, similar to long-range order in a pseudo-condensate75. Furthermore, as the open system has sustainable oscillations stabilized by very strong dissipation, i.e., quantum Zeno regime, the model is a dissipative time crystal, as well.

Here, we report an exactly solvable model describing a broad class of driven-dissipative and interacting fermionic chains that shows quantum multistablity related to the strong symmetries of the Liouvillian. In general, the strong symmetries are not necessary for the existence of multistability (as degenerate stationary states may emerge in the thermodynamic limit only without a strong symmetry), nor are they sufficient since all of the degenerate stationary states implied by the strong symmetries may have the same expectation values for local observables. More generally, multistability is taken to be an effect not due to any manifest symmetry. However, in our case emergent strong symmetries do guarantee multistability in local observables. In contrast to other potentially bistable models27, here, rather than being detrimental, quantum fluctuations are essential for the multistability. Further, we show that for certain types of jump operators the Liouvillian has dynamical symmetries that lead to sustainable oscillations in the non-equilibrium long-time behavior of the system, a phenomenon known as dissipative time crystal. Our approach is based on identifying a novel modulated76 spectrum generating algebra (SGA)77, which is non-local and fermionic. Since standard dynamical symmetries31 are extensive and local SGA78,79 and the SGA here is extensive and semi-local in spin, we call it a semi-local dynamical symmetry80. This dynamical symmetry, being fermionic, cannot be relegated to a non-Abelian symmetry, unlike previously known cases based on closed algebras settling the question of whether such operator relations are possible81. Later, for sake of simplicity, we specialize the general dissipative-driven fermionic model to a quadratic model and show that these models have an infinite set of emergent (thermodynamic) super-extensive raising operators that we call super-extensive dynamical symmetries. We provide evidence that the total effect of all these operators is that the model displays very slow finite-size decay due to the presence of strong symmetries82, which guarantee degenerate stationary states (null space of Liouvillian). These have attracted lots of interest recently due to their utility for quantum information storage 83,84,85,86,87,88,89,90,91,92,93,94,95,96. Moreover, as this behavior is robust to a wide-class of perturbations and occurs in the thermodynamic limit any for generic parameter values, it also constitutes the first example of a boundary time crystal, to the best of our knowledge, in an short-range interacting model. We also derive an analytical lower bound for the decay of such behaviors when the dynamical symmetry is not exact. Finally, we support our theoretical findings using a phase space approach to numerically calculate the Liouvillain spectrum as well as the correlation functions dynamics of the open quantum system dynamics highlighting the emergence of the dissipative time crystalline and the quantum multistabiliy as well as the scaling with the system size.

Results and discussion

The model

Consider the following interacting Kitaev chain model97,

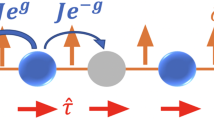
$$H= -\frac{1}{2}\mathop{\sum }\limits_{i=1}^{N}\left(w{c}_{i}^{{{\dagger}} }{c}_{i+1}+\Delta {c}_{i}{c}_{i+1}\right)+H.c.+\mu \mathop{\sum}\limits_{i}{n}_{i}\\ +V\mathop{\sum}\limits_{j}({c}_{j}+{c}_{j}^{{{\dagger}} })({c}_{j+1}+{c}_{j+1}^{{{\dagger}} })({c}_{j+2}+{c}_{j+2}^{{{\dagger}} })({c}_{j+3}+{c}_{j+3}^{{{\dagger}} }),$$
(1)

with \({c}_{j}^{{{\dagger}} }\) and cj being the (Dirac) fermionic creation and annihilation operator, w is the hopping amplitude, Δ is the p-wave pairing correlation, μ is the on-site chemical potential, and V is a novel interacting (beyond-quadratic in general) term we use to model the stronly interaction Majorana fermions, physically originated from electron-electron interactions98. The number operators are \({n}_{j}={c}_{j}^{{{\dagger}} }{c}_{j}\) and the chain is subject to the periodic boundary condition, i.e., cN+1 = c1. We note that complex values of coupling coefficients can be physically realized with e.g., constant phase gradients99 or laser coupling as recently employed in the simulation of a bosonic ladder100.

This model is commonly mapped onto a spin-1/2 transverse field Ising model at V = 0101. Note that the model we consider here is not mappable to integrable XYZ spin chains or noninteracting models in contrast to other interesting results102,103.

As will be apparent shortly, it is convenient to define Majorana fermion operators as,

$${\gamma }_{2j-1}={c}_{j}+{c}_{j}^{{{\dagger}} }\qquad {\gamma }_{2j}=i({c}_{j}-{c}_{j}^{{{\dagger}} }).$$
(2)

These fulfill the following anti-commutation relations,

$$\{{\gamma }_{j},{\gamma }_{m}\}=2{\delta }_{jm}.$$
(3)

Furthermore, here we will study a dissipative case with an incoherent Markovian driving modeled by a Lindblad master equation,

$$\frac{d\rho }{dt}=\hat{{{{{{\mathcal{L}}}}}}}[\rho ],$$
(4)

where \(\hat{{{{{{\mathcal{L}}}}}}}\) is a quantum Liouvillian of the form

$$\hat{{{{{{\mathcal{L}}}}}}}[\rho ]=-{{{{{\rm{i}}}}}}[H,\rho ]+\mathop{\sum}\limits_{\mu }\left(2{L}_{\mu }\rho {L}_{\mu }^{{{\dagger}} }-\{{L}_{\mu }^{{{\dagger}} }{L}_{\mu },\rho \}\right),$$
(5)

and the Lindblad jump operators are local Majorana dissipation, as incoherent local single-fermion drive and dissipation of the form \({L}_{j,1}=\sqrt{\Gamma }({c}_{j}^{{{\dagger}} }+{c}_{j})=\sqrt{\Gamma }{\gamma }_{2j-1}\), j = 1, …N. The quadratic version of this model (V = 0) has been previously studied for its topological properties104. We will also consider a special type of dissipative pairing as \({L}_{j,2}=\sqrt{\varepsilon }({c}_{j}+{c}_{j}^{{{\dagger}} })({c}_{j+1}+{c}_{j+1}^{{{\dagger}} })=\sqrt{\varepsilon }\,{\gamma }_{2j-1}{\gamma }_{2j+1}\) which can be engineered with Pauli blocking105.

It is useful to define a vector space of operators with the standard Hilbert-Schmidt inner product, as \(\langle \langle A| B\rangle \rangle ={{{{{\rm{tr}}}}}}({A}^{{{\dagger}} }B)\), with a corresponding norm that we will use.

In order to solve the dynamics of ρ(t) it is useful to diagonalize \(\hat{{{{{{\mathcal{L}}}}}}}\). Define λk to be the eigenvalues of \(\hat{{{{{{\mathcal{L}}}}}}}\) and ρk, σk to be the corresponding right and left eigenoperators, respectively,

$$\begin{array}{c}\hat{{{{{{\mathcal{L}}}}}}}[{\rho }_{k}]={\lambda }_{k}{\rho }_{k},\,{\hat{{{{{{\mathcal{L}}}}}}}}^{{{\dagger}} }[{\sigma }_{k}]={\lambda }_{k}^{* }{\sigma }_{k},\\ \langle \langle {\sigma }_{k}| {\rho }_{{k}^{{\prime} }}\rangle \rangle ={\delta }_{k,{k}^{{\prime} }}.\end{array}$$
(6)

Due to the semi-group properties of the Lindblad master equation all the eigenoperators are either stable or decaying, i.e., Re(λk) ≤ 0. Further, they always appear in complex conjugate pairs as \(\{{\lambda }_{k},{\lambda }_{k}^{* }\}\). Since the jump operators Lμ are Hermitian in our model, the Lindblad equation is unital, and the identity matrix is always a non-equilibrium steady state (NESS), i.e., \({\rho }_{0}={\mathbb{1}}\).

We are interested in the dynamics of observables O(t) when we initalize the system in ρ(0). Formally, the solution can be written as

$$\langle O(t)\rangle =\mathop{\sum}\limits_{k}{e}^{t{\lambda }_{k}}\langle \langle O| {\rho }_{k}\rangle \rangle \langle \langle {\sigma }_{k}| \rho (0)\rangle \rangle .$$
(7)

Purely imaginary eigenvalues are therefore necessary but not sufficient for persistent oscillations in physical observables due to possibly vanishing overlap of local observables with right eigenoperator, or the zero overlap of the initial state with left eigenoperators, or the presence of dense and incommensurate purely imaginary eigevalues λk in the Liouvillian spectrum.

Emergent dynamical symmetries in the thermodynamic limit

The origin of dynamical symmetries can be understood by studying the quadratic version of the model in (1) in the noninteracting limit, i.e., H0 = H(V = 0). The model is then the standard Kitaev Hamiltonian that in the thermodynamic limit can be diagonalized with a Fourier transform followed by a Bogoliubov transformation. We obtain (up to an irrelevant shift),

$${H}_{0}=\mathop{\sum}\limits_{k}{E}_{k}\,{d}^{{{\dagger}} }(k)d(k),$$
(8)

with the lowering operators of,

$$ d(k)={u}_{k}c(k)+{v}_{k}{c}^{{{\dagger}} }(-k),\\ c(k)=\frac{{e}^{-{{{{{\rm{i}}}}}}\frac{\pi }{4}}}{\sqrt{N}}\mathop{\sum }\limits_{j=1}^{N}{e}^{-{{{{{\rm{i}}}}}}kj}{c}_{j}.$$
(9)

Here, c(k) is the Fourier transform of the fermion annihilation operator at momentum k and d(k) is its Bogoliubov transformation where the (not-normalized) coefficients are defined as

$$ {u}_{k}=-\frac{{{{{{\rm{i}}}}}}\Delta \sin (k)\sqrt{{E}_{k}-w\cos (k)-\mu }}{\sqrt{2}\left\vert \Delta \sin (k)\right\vert \sqrt{{E}_{k}}},\\ {v}_{k}=\frac{{{{{{\rm{i}}}}}}({E}_{k}+w\cos (k)+\mu )}{\Delta \sin (k)}{u}_{k},$$
(10)

and the energy is,

$${E}_{k}=\sqrt{{\left\vert \Delta \sin (k)\right\vert }^{2}+{(w\cos (k)+\mu )}^{2}}.$$
(11)

The momentum is restricted to the first Brillouin zone \(k=\frac{2\pi }{N}m\), \(m=-\frac{N}{2}+1,\ldots ,\frac{N}{2}-1,\frac{N}{2}\).

If for some κ, uκ = − vκ, we have up to a multiplicative constant,

$${d}_{\kappa }=\mathop{\sum }\limits_{j=1}^{N}{e}^{-{{{{{\rm{i}}}}}}\kappa j}{\gamma }_{2j}.$$
(12)

Solving uk = − vk using (10) for purely imaginary Δ gives \(\kappa ={\cos }^{-1}(-\frac{\mu }{w})\), which is a real momentum for \(\left\vert \mu \right\vert < \left\vert w\right\vert \), coinciding with the topological phase of the Kitaev chain. Using (3) it is clear that even Majorana fermions γ2j commute with any product of an even number of odd Majorana fermions γ2j−1. That means the interaction term of the Hamiltonian in (1) commutes with dκ from which it directly follows that,

$$[H,{d}_{\kappa }]=-{E}_{\kappa }{d}_{\kappa },$$
(13)

where \({E}_{\kappa }=\left\vert \Delta \sqrt{1-\frac{{\mu }^{2}}{{w}^{2}}}\right\vert \).

Thus dκ is a modulated fermionic dynamical symmetry of the model. They are essentially similar to Goldstone modes, except they exist at finite frequency and momentum. The dynamical symmetry implies that observables with non-zero overlap with it can persistently oscillate at frequency Eκ81. Note that there are special values of parameters for which the dynamical symmetries exist for finite systems, e.g., for μ = 0, κ = π/2 is always a solution for mod(N, 4) = 0. For more general μ, w (with ∣μ∣ < ∣w∣); however, the dynamical symmetries exist only in the thermodynamic limit as for finite systems there is no solution for κ for general μ, w. In other words, these dynamical symmetries are emergent for systems that are large enough to have a continuum of momenta k in the 1st B.Z. Hence, they are thermodynamically emergent symmetries.

Now consider the case Γ = 0. Since the jump operators Lj,2 are as sums of products of odd Majorana fermions one has [Lj,2, dκ] = 0. Therefore, S ≔ dκ is an emergent strong dynamical symmetry of the open quantum system with dissipators Lj,2 in the thermodynamic limit31,106,107, which implies that operators \({S}^{n}{\rho }_{\infty }{({S}^{{{\dagger}} })}^{m}\) are eigenoperators of \(\hat{{{{{{\mathcal{L}}}}}}}\) with purely imaginary eigenvalues i(n − m)Eκ. Here, n, m = 0, ± 1 as \({S}^{2}={\mathbb{1}}\). Note that S is local in the fermion basis in the sense of being a sum of local densities.

Here, the eigenstate dephasing108 is not possible because the purely imaginary eigenspectrum is equally spaced. In order to qualify as a boundary time crystal the system must, in addition to the previous conditions, have persistent oscillations in local observables47. This is the case because S is local and has non-zero overlap with local observables meaning that the expectation values of a local observable (by (7)),

$$\mathop{\lim }\limits_{t\to \infty }\langle O(t)\rangle ={{{{{\rm{tr}}}}}}[O\mathop{\sum}\limits_{n,m}{e}^{{{{{{\rm{i}}}}}}(n-m){E}_{\kappa }}{c}_{n,m}{S}^{n}{\rho }_{\infty }{({S}^{{{\dagger}} })}^{m}],$$
(14)

will be finite and persistently time-periodic in the thermodynamic limit. This is clearest when considering the example O = γ2j with the asymptotic state \(\rho (t)={\mathbb{1}}+{e}^{{{{{{\rm{i}}}}}}{E}_{\kappa }t}S+{e}^{-{{{{{\rm{i}}}}}}{E}_{\kappa }t}{S}^{{{\dagger}} }\).

This therefore constitutes, an exact example of a boundary time crystal in an extended many-body system with local interactions. Besides, we conjecture that the model is a dissipative time crystal as well (persistent oscillations induced by dissipation) because the closed model likely has oscillations that dephase due to the multitude of incommensurate eigenvalues108. We will discuss robustness of the boundary time crystal state in the next section.

Semi-local dynamical symmetries and stability of the dynamics

We will now consider the case when Γ ≠ 0 and in order to simplify the following discussion we will assume without loss of generality that the parameters of the model are such that the dynamical symmetry exists for some finite values of N, e.g., at μ = 0 as discussed in the previous subsection.

Let us define \({m}_{j}=\frac{1}{2}{\mathbb{1}}-{n}_{j}\) and the parity operator \({P}_{j,k}=\mathop{\prod }\nolimits_{q = j}^{k}{m}_{q}\). We now note some useful identities. The Hamiltonian is parity-symmetric, i.e., [H, P1,N] = 0, and the Lindblad jump operators are parity-antisymmetric, i.e., {Lμ,1, P1,N} = 0 and furthermore satisfy {Lμ,1, dκ} = 0. From this it follows directly that [H, P1,Ndκ] = − EκP1,Ndκ and [Lμ,1, P1,Ndκ] = 0 hence, \({A}^{{\prime} }={P}_{1,N}{d}_{\kappa }\) is a non-local strong spectrum generating algebra.

Remark 1: As a side note we will show that this operator leads to a semi-local dynamics symmetry when mapped to the spin systems.

Here, for reasons that will become apparent, we consider the standard Wigner-Jordan mapping109,

$$\begin{array}{l}{\tilde{P}}_{j,k}=\mathop{\prod }\nolimits_{x = j}^{k}{\sigma }_{x}^{z},\\ {c}_{j}={\tilde{P}}_{1,j-1}{\sigma }_{j}^{-}.\end{array}$$
(15)

Following the mapping in (15), operator \({A}^{{\prime} }\) gets transformed to a semi-local dynamical symmetry in the spin basis, i.e., its densities commute only with operators on one side of the chain with the following form,

$${\tilde{A}}^{{\prime} }=\mathop{\sum }\limits_{j=1}^{N}\exp ({{{{{\rm{i}}}}}}\frac{\pi }{2}j){\sigma }_{j}^{x}{\tilde{P}}_{j+1,N}.$$
(16)

Such semi-local symmetry operators have been studied recently in the context of generalized hydrodynamic corrections in quadratic and integrable models where their existence was associated with the topological nature of the models80. Topology likely plays a role in our model as it is intimately related to the Kitaev chain. These new kinds of dynamical symmetries should be distinguished from both local extensive78,110,111,112 and strictly local ones113,114,115. We emphasize, that in the model studied here there is no obvious transformation that would allow mapping this semi-local dynamical symmetry into a semi-local non-Abelian symmetry while preserving the spatial locality of H.

The operators \({A}^{{\prime} }\) and \({({A}^{{\prime} })}^{{{\dagger}} }\) satisfy fermionic anti-commutation relations \(\{{A}^{{\prime} },{({A}^{{\prime} })}^{{{\dagger}} }\}={\mathbb{1}}\) and they are nilpotent \({({A}^{{\prime} })}^{2}=0\).

The existence of \({A}^{{\prime} }\) immediately implies the existence of a super-extensive (quadratic) charge \(Q={({A}^{{\prime} })}^{{{\dagger}} }{A}^{{\prime} }\) for which it can be easily shown that \({{{{{\rm{tr}}}}}}({Q}^{2})/{2}^{N}\propto {N}^{2}\) by observing that the expression has only finite trace for those term in the doubled sum when local densities are on the same site. For example, for μ = 0, in the Majorana basis it may be written as,

$$Q={{{{{\rm{i}}}}}}\left(\mathop{\sum }\limits_{j=1}^{N}{{{{{{\rm{i}}}}}}}^{j-1}{\gamma }_{2j}\right)\left(\mathop{\sum }\limits_{j=1}^{N/2}{(-1)}^{j}{\gamma }_{4j}\right).$$
(17)

This Hermitian operator defines a symmetry S = eiQ as [H, S] = 0. We remark that for the closed system (Γ = ϵ = 0), the existence of Q and its growth with system size immediately implies that the memory of the initial state decays as 1/N2 in local observables O with \({{{{{\rm{tr}}}}}}(QO)\,\ne \,0\) as quantified by e.g., infinite temperature auto-correlation functions 〈O(t)O〉 via the Mazur bound116.

For the open system, S is a strong symmetry82,117, which in turn implies that the non-equilibrium stationary state λ0 = 0 is degenerate. There, \({\rho }_{0}^{{\prime} }={{{{{\bf{1}}}}}}-({A}^{{\prime} }{({A}^{{\prime} })}^{{{\dagger}} })\) is the other eigenoperator of the Liouvillian null space for λ0 = 0 where we define \({{{{{\bf{1}}}}}}:= {\mathbb{1}}/({2}^{N}tr[({A}^{{\prime} }{({A}^{{\prime} })}^{{{\dagger}} })])\), in order for it to be Hilbert-Schmidt orthogonal to the left null space eigenmode \({\omega }_{0}={\mathbb{1}}\), i.e., \(tr({\rho }_{0}^{{\prime} })=0\). It is worth reminding that due to unitality of the Liouvillian, one NESS is always \({\rho }_{0}=1/{2}^{N}{\mathbb{1}}\).

Furthermore, based on the properties of \({A}^{{\prime} }\), \({\rho }_{1}={({A}^{{\prime} })}^{{{\dagger}} }\), \({\rho }_{-1}={A}^{{\prime} }\) are the bi-orthogonal eigenmodes corresponding to the purely imaginary eigenvalues of λ±1 = iEκ. Due to unitality the left and right eigenmodes are each others conjugate transposes, i.e., \({\sigma }_{\mp 1}={{{{{\mathcal{N}}}}}}{({\rho }_{\pm 1})}^{{{\dagger}} }\) up to a normalization constant \({{{{{\mathcal{N}}}}}}\).

It is obvious that the presence of purely imaginary eigenvalues is not visible in any local observable O because \({A}^{{\prime} }\) is non-local as it does not contain any local terms hence, ρ±1 do not have Hilbert-Schmidt overlap with such observables.

The multistability situation is different however, as \({\rho }_{0}^{{\prime} }\) has a non-zero overlap with a local observable O (without loss of generality tr(O) = 0). In order to estimate its multistability, we first note that a general stationary state must be density matrix and hence a convex combination of the two stationary states \({\rho }_{\infty }={\rho }_{0}={\rho }_{0}+c{\rho }_{0}^{{\prime} }\) such that ρ∞ is positive semi-definite.

Because ∣∣ρ0∣∣2 = 1/2N, \(| | {\rho }_{0}^{{\prime} }| {| }^{2}\propto {N}^{2}/{2}^{N}\) and the eigenvalues of \({\rho }_{0}^{{\prime} }\) sum into 0 by construction, c ∝ 1/N. However, since for local observables \({{{{{\rm{tr}}}}}}(O{\rho }_{0}^{{\prime} })\propto {N}^{0}\) we have for the expectation values,

$$\langle O(t\to \infty )\rangle \propto \langle \langle O| c{\rho }_{0}^{{\prime} }\rangle \rangle \propto 1/N,$$
(18)

which gives a lower bound on the ∣〈O(t → ∞)〉∣. We note that this is only a lower bound because many eigenvalues have vanishing real part in the limit of N → ∞ and hence the actual expectation values can decay slower with N. Thus the model is bistable only for the finite-sized chains where quantum fluctuations are important. This is unlike typical mean-field multistability scenarios occurring in the thermodynamic limit (i.e., N → ∞) where quantum fluctuations do not play a role.

Expanding for small ε = O(1/N) around k = κ ± ε we have \([{L}_{\mu },{P}_{1,N}{d}_{\kappa \pm \varepsilon }]={{{{{\mathcal{O}}}}}}(\varepsilon )\) (by Taylor series expansion) and, likewise, [H, dκ±ε] = − Eκdκ + O(ε). As ε ∝ 1/N, this implies that the dissipative gap (the real part of the eigenvalues of the Liouvillian) closes as ∝ 1/N into the same purely imaginary eigenvalues. They are hence metastable118,119,120. We will confirm this in the next section with a concrete example. The closing of the Liouvillian gap is associated with an algebraic temporal relaxation of the dynamics, but as we will see in the next section, it can also lead to larger quantum fluctuations (i.e., slower decay of multistability with N). Therefore, these additional dynamical symmetry lead to a different behavior than the standard power-law decay of multistability and oscillations that are usually studied for Liouvillian gaps closing121,122,123.

It is important to note that, even though \({A}_{\kappa }^{2}=0\), Aκ+εAκ ≠ 0 and thus these operators do have overlap with local operators (this follows from \({P}_{1,N}^{2}={\mathbb{1}}\)), leading to boundary pseudo-time crystal behavior in local observables as will be shown in the numerical results subsection.

The dynamical symmetries are responsible for both the boundary (pseudo-)crystal and the multistability. As long as the dynamical symmetries we discovered are present these phenomena will be as well. The semi-local dynamical symmetries are completely non-perturbatively stable to all perturbations that are odd in the Majorana fermions i.e., \({D}_{x}={\sum }_{j}{x}_{j}^{(1)}{\gamma }_{2j-1}+{x}_{j,k}^{(2)}{\gamma }_{2j-1}{\gamma }_{2k-1}\ldots \) for arbitrary parameter set x. Namely, lets introduce an arbitrary such perturbation H → H + Dx, Lk,μ → Lk,μ + Dk,y. We will still have \([H,{A}^{{\prime} }]={E}_{k}\kappa {A}^{{\prime} }\) and \([{L}_{k,\mu },{A}^{{\prime} }]=[{L}_{k,\mu }^{{{\dagger}} },{A}^{{\prime} }]=0\) and \({A}^{{\prime} }\) remains a strong dynamical symmetry. What if the perturbation W is even in the Majorana fermions i.e., H → H + sW, Lk,μ → Lk,μ + sW? In that case the purely imaginary are stable at least to the second order in the small parameter s according to the results of ref. 106. Hence, an degree of sub-leading stability remains.

Moreover, according to the results of ref. 106 if we can engineer ϵ to be large a quantum Zeno dynamics will emerge. More specifically, the purely imaginary eigenvalues will be stable up to corrections 1/ϵ2 that we can engineer to be small. In other words, the dissipation will stabilize the oscillations to any perturbations. This renders the system a dissipative time crystal in the sense of dissipation inducing persistent oscillations in the our many-body system31.

Numerical results

In this section, for sake of simplicity, we will focus on the quadratic model, noting that the general conclusion, according to the discussion in the previous sections, holds for the interacting models, as well.

Besides, as the open system with Lμ,2 jump operators leads to an exact time-periodic behavior as discussed here we merely focus on Lμ,1 dissipators to show the finite-size scaling.

To check the existence of the pure imaginary eigenvalues λk and find the multiplicity of the null space, we employ the third quantization method for calculating the Liouvillian spectrum for N-fermion chains where \(\,{{{{\mathrm{mod}}}}}\,\,(N,4)=0\) subject to the periodic boundary conditions, as described in the model subsection. As the conserved dynamics is quadratic and the jump operators are linear in fermionic basis the Liouville super-operator (\({{{{{\mathcal{L}}}}}}\)) can be diagonalized in terms of 2N normal master modes acting on the Fock states of density operators124. The eigenvalues of the super-operator (λk) can be obtained directly from the spectrum of the shape matrix, aka rapidities (βi) as

$$\,{\lambda }_{\overrightarrow{v}}=-2\mathop{\sum }\limits_{i=1}^{2N}{\beta }_{i}{v}_{i},$$
(19)

where \(\overrightarrow{v}\) is a 2N-long binary string. An alternative approach, also finding a closing spectral gap in related models, can be found in125.

The whole Liouvillian spectrum can be exactly calculated by considering all \(\overrightarrow{v}\) within (1, 4N). Due to the linear growth of the shape matrix with N, in opposed to an exponential one, one can obtain detailed information about \({{{{{\mathcal{L}}}}}}\) without being limited to small N chains hence, an equal treatment of the finite-sized systems and larger one approaching the thermodynamic limit (cf. the methods section further details).

Figure 1a–c shows the Liouvillian spectrum (λk) of noninteracting Kitaev model in (1) for μ = 0, w = 1, Δ = i at different chain lengths of N = 4, 12, and 100, respectively. For cases (b) and (c) the spetrum is zoomed in close to the imaginary axis to highlight the slowly decaying eigenvalues. The red dots show the pure imaginary eigenvalues at λ± = ± 2i, and the green dot corresponds to the degenerate NESS at λ0 = 0.

Fig. 1: Liouvillian gap closure and the signature of the non-stationary phase.
figure 1

Liouvillian spectrum of noninteracting Kitaev chain for different chain length a N = 4, b N = 12, and c N = 100 subject to periodic boundary conditions. In all cases the chemical potential, hopping amplitude, and pairing potential are μ = 0, w = 1, Δ = i, respectively. The red and green dots show the pure imaginary and zero eigenvalues, respectively.

Full size image

To examine the multistability and the long-time behavior of the system we study the two-point correlations and their time evolution. As the whole dynamics, including both the conservative and the dissipative part, is quadratic the state is Gaussian hence its first and second moments (two-point correlation functions) are sufficient to describe the system, fully. Using the Heisenberg picture we can derive the following equations of motion for the two-point correlation functions

$$\frac{d}{dt}\langle {c}_{m}{c}_{n}\rangle = {{{{{\rm{i}}}}}}\Big(w\langle {c}_{m+1}{c}_{n}\rangle +w\langle {c}_{m}{c}_{n+1}\rangle +{w}^{* }\langle {c}_{m-1}{c}_{n}\rangle +{w}^{* }\langle {c}_{m}{c}_{n-1}\rangle \\ +2\mu \langle {c}_{m}{c}_{n}\rangle -{\Delta }^{* }\langle {c}_{n}{c}_{m+1}^{{{\dagger}} }\rangle +{\Delta }^{* }\langle {c}_{n}{c}_{m-1}^{{{\dagger}} }\rangle \Big) \\ +{{{{{\rm{i}}}}}}\left({\Delta }^{* }\langle {c}_{m}{c}_{n+1}^{{{\dagger}} }\rangle -{\Delta }^{* }\langle {c}_{m}{c}_{n-1}^{{{\dagger}} }\rangle \right)\\ +2\mathop{\sum}\limits_{k}{\gamma }_{k}\left(\left(\langle {c}_{k}\rangle +\langle {c}_{k}^{{{\dagger}} }\rangle \right)\left(\langle {c}_{m}\rangle {\delta }_{nk}-\langle {c}_{n}\rangle {\delta }_{mk}\right)\right),$$
(20)
$$\frac{d}{dt}\langle {c}_{m}^{{{\dagger}} }{c}_{n}\rangle = {{{{{\rm{i}}}}}}\Big(-w\langle {c}_{m-1}^{{{\dagger}} }{c}_{n}\rangle +w\langle {c}_{m}^{{{\dagger}} }{c}_{n+1}\rangle -{w}^{* }\langle {c}_{m+1}^{{{\dagger}} }{c}_{n}\rangle +{w}^{* }\langle {c}_{m}^{{{\dagger}} }{c}_{n-1}\rangle \\ +\Delta \langle {c}_{m-1}{c}_{n}\rangle -\Delta \langle {c}_{m+1}{c}_{n}\rangle \Big)+{{{{{\rm{i}}}}}}\left(-{\Delta }^{* }\langle {c}_{m}^{{{\dagger}} }{c}_{n-1}^{{{\dagger}} }\rangle +{\Delta }^{* }\langle {c}_{n+1}^{{{\dagger}} }{c}_{m}^{{{\dagger}} }\rangle \right)\\ +2\mathop{\sum}\limits_{k}{\gamma }_{k}\left(\left(\langle {c}_{n}\rangle {\delta }_{mk}-\langle {c}_{m}^{{{\dagger}} }\rangle {\delta }_{nk}\right)\left(\langle {c}_{k}\rangle +\langle {c}_{k}^{{{\dagger}} }\rangle \right)\right).$$
(21)

As can be seen, correlations make a closed set of coupled nonlinear equations that can be numerically solved knowing the initial states.

The time evolution of a local two-point correlation (\(\langle {\hat{c}}_{1}{\hat{c}}_{2}\rangle \)) of such chains is presented in Fig. 2 showcasing the emergence of both non-stationary steady states, aka dissipative time crystal, and the multistability, manifested by two distinct values at long-time limit. Since the long-time solutions in the bistable region depend on the initial state (cf. (7)), the equations of motion as in (20) and (21) are evolved for randomized initial states, two of them shown as red and blue lines in each panel.

Fig. 2: Multistability and non-stationary behavior vs. the system size.
figure 2

Time evolution of the first and the second site correlation (\(| \langle {\hat{c}}_{1}{\hat{c}}_{2}\rangle | \)) showcasing the multistability for two randomized initial states and the oscillatory behavior for various chain length of a N = 4, b N = 12, and c N = 100 subject to the periodic boundary condition. Blue and red lines correspond to two different randomized initial conditions.

Full size image

To examine the scaling of the local observable with the system size (N) in Fig. 3 we plot the long-time value of \(| \langle {\hat{c}}_{1}{\hat{c}}_{2}\rangle | \) as a function of the chain length.

Fig. 3: Observable scaling with the system size.
figure 3

Local observable scaling vs. the chain length N when the initial correlation in all cases is the same as two-site correlation of \(\langle {\hat{c}}_{n}{\hat{c}}_{m}\rangle =1+i\) and initial occupation of \(\langle {\hat{c}}_{n}^{{{\dagger}} }{\hat{c}}_{n}\rangle =1\). The dots are the results of the moments equations of motion integration, the dashed line is guide to the eye, and the red line is N−1 scaling for comparison.

Full size image

The dots show the results of the numerical calculations when the initial correlations are chosen to be \(\langle {\hat{c}}_{n}{\hat{c}}_{m}\rangle =1+{{{{{\rm{i}}}}}}\) and \(\langle {\hat{c}}_{n}{\hat{c}}_{n}^{{{\dagger}} }\rangle =0\), i.e., having one particle on each site. As can be seen the correlation for smaller system sizes follows a power-law behavior decaying as N−1 (red line in Fig. 3) consistent with the lower bound prediction of the semi-local dynamical symmetries and stability of the dynamics subsection. For longer chains, i.e., larger N, more semi-local dynamical symmetries (semi-local finite-frequency Goldstone modes) start emerging and the decay with N slows down, consistent with the results of the emergent dynamical symmetric in the thermodynamic limit subsection. More specifically,

$$\langle O(t\to \infty )\rangle =\mathop{\sum}\limits_{k}{e}^{t({{{{{\rm{i}}}}}}{\omega }_{k}+{{{{{\mathcal{O}}}}}}(1/N))}\langle \langle O| {\rho }_{k}\rangle \rangle \langle \langle {\sigma }_{k}| \rho (0)\rangle \rangle .$$
(22)

with \({\omega }_{k}\in {\mathbb{R}}\) and the complex decay rate goes down as \({{{{{\mathcal{O}}}}}}(1/N)\)). This implies both multistability and the persistent oscillations.

Conclusions

In this paper we have shown that for large classes of driven strongly interacting models there exist spectrum generating algebras that are semi-local in the spin basis, which we therefore named semi-local dynamical symmetries. They generically are manifest in the thermodynamic limit only. Physically, they correspond to particle excitations that are invisible to the interaction. They also imply non-local (quadratic) conservation laws, which are promoted to strong symmetries when the system is subjected to pair dephasing. Being quadratic, these operators directly imply memory of the initial condition, i.e., degenerate stationary states and multistability that decays with system size. This means that, unlike previously studied cases of multistability, here the multistability is present in the quantum fluctuations and in the finite-size systems (beyond mean-field) rather than being destroyed by them. Our work implies that genuine (fully exact) multistability for quantum many-body systems requires emergent symmetry structure in the thermodynamic limit, even though a manifest one is not necessarily present for the finite-size system.

The system in the thermodynamic limit obtains further emergent dynamical symmetries, which are finite-frequency and finite-momentum quasi-particles dressing the original dynamical symmetry excitations. Therefore, we call these emergent dynamical symmetries semi-local finite-frequency and finite-momentum Goldstone modes. For the dissipative system they imply strong symmetries. These Goldstone modes imply that, as we approach the thermodynamic limit, decay times of oscillations in the local observables diverge, but their amplitude goes to zero at least for initial states that have low-enough entanglement. Hence the system is a boundary time time crystal according to the thermodynamic requirements of ref. 47. However, the oscillations are clean and periodic both for the isolated (closed Lμ = 0) and dissipative system, therefore our system is not a dissipative time pseudo-time crystal in the sense of the dissipative time crystals introduced in ref. 31, which would imply that dissipation is the one inducing periodic oscillations absent for the isolated system.

To the best of our knowledge, this is the first exact and fully non-perturbative result on the long-debated problem of multistability and multistability in driven-dissipative many-body quantum systems. Although we studied pairing fermionic models, the approach of thermodynamically emergent dynamical symmetries implying quasi-particles that are invisible to certain kinds of interactions is general and can be applied to both bosonic and spin systems. Our work provides an approach for proving presence of multistability in more general and widely studied quantum optical setups.

In future works, we plan to apply our approach to many-body spin and bosonic systems where multistability and persistent oscillations have been experimentally observed in the thermodynamic limit. Exploring the underlying connection between emergent collective behaviors and topology in such systems with quantum synchronization106,126,127,128 are other interesting directions of the future studies.

Methods

Shape matrix, rapidities, and Liouvillian spectrum

As described in ref. 124 the two parts of the super-operator, i.e., the conserved dynamics \({\hat{{{{{{\mathcal{L}}}}}}}}_{H}\) and the non-unitary parts \({\hat{{{{{{\mathcal{L}}}}}}}}_{D}\) has the following forms

$$\,{{{{{{\mathcal{L}}}}}}}_{H}=-i4\mathop{\sum}\limits_{j,k}{\hat{c}}_{j}^{{{\dagger}} }{H}_{jk}{\hat{c}}_{k},$$
(23)

and

$${{{{{{\mathcal{L}}}}}}}_{D}^{+}=2\mathop{\sum }\limits_{j,k=1}^{2N}\mathop{\sum }\limits_{\mu =1}^{N}{l}_{\mu j}{l}_{\mu k}^{* }\left(2{\hat{c}}_{j}^{{{\dagger}} }{\hat{c}}_{k}^{{{\dagger}} }-{\hat{c}}_{j}^{{{\dagger}} }{\hat{c}}_{k}-{\hat{c}}_{k}^{{{\dagger}} }{\hat{c}}_{j}\right),$$
(24)

where \({\hat{c}}_{i},{\hat{c}}_{i}^{{{\dagger}} }\) are the super-operator (a-fermion) annihilation and creation operators in the operator Fock space, respectively. Here, we focus on the \({{{{{{\mathcal{K}}}}}}}^{+}\), i.e., the even sup-space, only.

We define the 4N × 1-vector of a-fermionic operators as

$$\hat{{{{{{\bf{C}}}}}}}=\left(\begin{array}{c}{\hat{c}}_{1}\\ \cdots \\ {\hat{c}}_{2N}\\ {\hat{c}}_{1}^{{{\dagger}} }\\ \cdots \\ {\hat{c}}_{2N}^{{{\dagger}} }.\end{array}\right)$$
(25)

With this definition we can write the Liouville super-operator \({\hat{{{{{{\mathcal{L}}}}}}}}^{+}={\hat{{{{{{\mathcal{L}}}}}}}}_{H}+{\hat{{{{{{\mathcal{L}}}}}}}}_{D}^{+}\) as

$$\,{\hat{{{{{{\mathcal{L}}}}}}}}^{+}={\hat{{{{{{\bf{C}}}}}}}}^{{{\dagger}} }{{{{{{\bf{L}}}}}}}^{+}\hat{{{{{{\bf{C}}}}}}}={\hat{{{{{{\bf{C}}}}}}}}^{{{\dagger}} }\left(\begin{array}{cc}{{{{{{\bf{L}}}}}}}_{11}&{{{{{{\bf{L}}}}}}}_{12}\\ {{{{{\bf{0}}}}}}&{{{{{{\bf{L}}}}}}}_{22}\end{array}\right)\hat{{{{{{\bf{C}}}}}}},$$
(26)

To write the non-unitary parts easier, we define a matrix with entries \({M}_{jk}=\mathop{\sum }\nolimits_{\mu = 1}^{N}{l}_{\mu j}{l}_{\mu k}^{* }\) hence, M = M† is a Hermitian matrix.

Using these definitions we have

$$ {{{{{{\bf{L}}}}}}}_{11}^{jk}=-i2{H}_{jk}-{M}_{jk}-{M}_{kj}=-i2{H}_{jk}-{M}_{jk}-{M}_{jk}^{{\prime} },\\ {{{{{{\bf{L}}}}}}}_{12}^{jk}=4{M}_{jk},\\ {{{{{{\bf{L}}}}}}}_{22}^{jk}=i2{H}_{kj}+{M}_{kj}+{M}_{jk}=-i2{H}_{jk}+{M}_{jk}^{{\prime} }+{M}_{jk}.$$
(27)

Considering the antisymmetric properties of H, it becomes apparent that \({{{{{{\bf{L}}}}}}}_{11}=-{{{{{{\bf{L}}}}}}}_{22}^{{{\dagger}} }\). Therefore, we have

$$\,{\hat{{{{{{\mathcal{L}}}}}}}}^{+}={\hat{{{{{{\bf{C}}}}}}}}^{{{\dagger}} }\left(\begin{array}{cc}-{{{{{{\bf{L}}}}}}}_{22}^{{{\dagger}} }&{{{{{{\bf{L}}}}}}}_{12}\\ {{{{{\bf{0}}}}}}&{{{{{{\bf{L}}}}}}}_{22}\end{array}\right)\hat{{{{{{\bf{C}}}}}}}.$$
(28)

The shape matrix A defined in124 is simply a rotation of this matrix hence, the eigenvalues of A and L+ are the same. If ηi, i ∈ {1, 2, ⋯  , 2N} are the eigenvalues of L22 then the eigenvalues of L+ appear in pairs as \(({\eta }_{i},-{\eta }_{i}^{* })\). Also from the form of L22 it is clear that the eigenvalues appear in complex conjugate pairs as \(({\gamma }_{i},{\gamma }_{i}^{* }),i\in \{1,2,\cdots \,,N\}\). Finally, one can conclude that the spectrum of the shape matrix A appear in quadruple of (ξ, ξ*, − ξ, − ξ*). The rapidities are defined as the subset of the eigenvalues with positive real parts from which the full spectrum of \({{{{{{\mathcal{L}}}}}}}^{+}\) can be obtained using (19). From this spectrum it becomes evident if there are any kernels, corresponding to multistability, or pure imaginary eigenvalues, corresponding to a non-stationary NESS.

Dispersion of a chain with periodic boundary conditions

Let’s consider an N-long chain with periodic boundary conditions (PBC), i.e., cm+N = cm. One can use the following Fourier transformation to find the spectral form

$$\tilde{c}(k)=\frac{1}{\sqrt{N}}\mathop{\sum}\limits_{m}{e}^{-imk}{c}_{m}\,,\,{c}_{m}=\frac{1}{\sqrt{N}}\mathop{\sum}\limits_{k}{e}^{imk}\tilde{c}(k).$$
(29)

It is straightforward to see that the anti-commutator relations of the Fourier series has the following form

$$\{\tilde{c}(k),\tilde{c}({k}^{{\prime} })\}=0\,,\,\{\tilde{c}(k),{\tilde{c}}^{{{\dagger}} }({k}^{{\prime} })\}={\delta }_{mn}\delta (k-{k}^{{\prime} }).$$
(30)

Replacing each term by its Fourier transform, we get the following spectral form

$$\tilde{H}(k)=\mathop{\sum}\limits_{k}-2| w| \cos (k+{\phi }_{w}){\tilde{c}}^{{{\dagger}} }(k)\tilde{c}(k)-\frac{\mu }{2}\left({\tilde{c}}^{{{\dagger}} }(k)\tilde{c}(k)-\tilde{c}(k){\tilde{c}}^{{{\dagger}} }(k)\right)$$
(31)
$$+\Delta {e}^{-ik}\tilde{c}(k)\tilde{c}(-k)+{\Delta }^{* }{e}^{-ik}{\tilde{c}}^{{{\dagger}} }(k){\tilde{c}}^{{{\dagger}} }(-k)$$
(32)
$$=\left({\tilde{c}}^{{{\dagger}} }(k)\,\tilde{c}(-k)\right)\left(\begin{array}{ccc}-| w| \cos (k+{\phi }_{w})-\frac{\mu }{2}&&i{\Delta }^{* }\sin k\\ -i\Delta \sin k&&| w| \cos (-k+{\phi }_{w})+\frac{\mu }{2}\end{array}\right)\left(\begin{array}{c}\tilde{c}(k)\\ {\tilde{c}}^{{{\dagger}} }(-k)\end{array}\right).$$
(33)

The choice of this spinor is useful since we can readily write the Fourier transform of Majorana fermions as a direct rotation

$$\,\left(\begin{array}{c}{\tilde{w}}_{o}(k)\\ {\tilde{w}}_{e}(k)\end{array}\right)=\left(\begin{array}{cc}1&1\\ i&-i\end{array}\right)\left(\begin{array}{c}\tilde{c}(k)\\ {\tilde{c}}^{{{\dagger}} }(-k)\end{array}\right),$$
(34)

where the o, e-superscripts refer to the odd and even Majorana fermions.

Substituting this back into the spectral Hamiltonian we can re-write it in terms of the Majorana fermions as

$${H}_{w}=\frac{1}{2}\left(\begin{array}{cc}| w| \sin {\phi }_{w}\sin k+{{{{{\rm{Im}}}}}}(\Delta )\sin k&i\left(| w| \cos {\phi }_{w}\cos k+\frac{\mu }{2}\right)-{{{{{\rm{Re}}}}}}(\Delta )\sin k\\ -i\left(| w| \cos {\phi }_{w}\cos k+\frac{\mu }{2}\right)-{{{{{\rm{Re}}}}}}(\Delta )\sin k&| w| \sin {\phi }_{w}\sin k-{{{{{\rm{Im}}}}}}(\Delta )\sin k\end{array}\right)$$
(35)

If the jump operators are identical for all fermionic sites as \({L}_{j}=\sqrt{g}\left({c}_{j}+\delta {c}_{j}^{{{\dagger}} }\right)\), then M will read as follows

$${{{{{\bf{M}}}}}}=\frac{g}{4}\left(\begin{array}{cc}| 1+\delta {| }^{2}&i\left(1-| \delta {| }^{2}\right)-2{{{{{\rm{Im}}}}}}(\delta )\\ -i\left(1-| \delta {| }^{2}\right)-2{{{{{\rm{Im}}}}}}(\delta )&| 1-\delta {| }^{2}\end{array}\right)$$
(36)

Finally, we can use (27) to determine the rapidities from the eigenvalues of \({{{{{{\bf{L}}}}}}}_{22}=-i2{{{{{\bf{H}}}}}}+{{{{{\bf{M}}}}}}+{{{{{{\bf{M}}}}}}}^{{\prime} }\). This leads to the following dispersion relation for rapidies as β(k)

$$\,\beta (k)=\frac{g}{4}\left(| 1+\delta {| }^{2}+| 1-\delta {| }^{2}\right)-i| w| \sin {\phi }_{w}\sin k+\pm \frac{1}{2}\sqrt{\Lambda },$$
(37)

where

$$\Lambda ={{{{{\rm{i}}}}}}4g\left(| 1+\delta {| }^{2}-| 1-\delta {| }^{2}\right){{{{{\rm{Im}}}}}}(\Delta )\sin k-4{\left(| w| \cos {\phi }_{w}\cos k+\frac{\mu }{2}\right)}^{2}-16| \Delta {| }^{2}{\sin }^{2}k$$
(38)
$$+{{{{{\rm{i}}}}}}16g{{{{{\rm{Re}}}}}}(\Delta ){{{{{\rm{Im}}}}}}(\delta )\sin k+\frac{{g}^{2}}{4}\left(| 1+\delta {| }^{4}+| 1-\delta {| }^{4}\right)-\frac{{g}^{2}}{2}| 1-{\delta }^{2}{| }^{2}+4{g}^{2}{{{{{\rm{Im}}}}}}{(\delta )}^{2}.$$
(39)