Anisotropic Fabry-Pérot resonant states confined within nano-steps on the topological insulator surface

Abstract

The peculiar nature of topological surface states, such as absence of backscattering, weak anti-localization and quantum anomalous Hall effect, has been demonstrated mainly in bulk and film of topological insulator (TI), using surface sensitive probes and bulk transport probes. However, it is equally important and experimentally challenging to confine massless Dirac fermions with nano-steps on TI surfaces. This potential structure has similar ground with linearly-dispersed photons in Fabry-Pérot resonators, while reserving fundamental differences from well-studied Fabry-Pérot resonators and quantum corrals on noble metal surfaces. In this paper, we study the massless Dirac fermions confined within steps along the x (Γ–K) or y (Γ–M) direction on the TI surface and the Fabry-Pérot-like resonances in the electronic local density of states (LDOS) between the steps are found. Due to the remarkable warping effect in the topological surface states, the LDOS confined in the step-well running along Γ-M direction exhibit anisotropic resonance patterns as compared to those in the step-well along Γ-K direction. The transmittance properties and spin orientation of Dirac fermion in both cases are also anisotropic in the presence of warping effect.

Introduction

Recently, the discovery of both two-dimensional and three-dimensional topological insulators (TIs)^1,2 has attracted enormous attentions. Unlike the conventional two-dimensional electron states, the spin-helical surface states of three-dimensional TIs, which are protected by the time-reversal symmetry and consist of an odd number of spin-helical Dirac cones, are characterized by the gapless Dirac Hamiltonian. Owing to the chiral nature of the quasiparticles in TI surface, many unusual effects have been observed. Among them, the quantum anomalous Hall effect has been theoretically³ predicted and experimentally⁴ observed in a thin films of chromium-doped TI material (Bi,Sb)₂Te₃, which may open a door of the application of TI materials in the field of the low-power-consumption electronics. A robust response of weak antilocalization^5,6,7 has been tested in the transport studies and the suppression of the backscattering has also been confirmed by examining the scattering from impurities or step edges^{8,9,10,11,12,13,14,15,16,17,18} in previous scanning tunneling microscopy (STM) reports. Particularly, because of the warping effect¹⁹ in topological surface states, the step scattering induced Friedel oscillations in the local density of states (LDOS) exhibit quite unique decaying power law^11,12 as compared to that in noble metals^20,21,22,23 and graphene²⁴. Furthermore, with the advanced progress of STM technologies, it is possible to study the optics-analogous properties of the quantum interference as well as quantum confinement of the conventional two-dimensional electron gas on noble metals^25,26. Recently, many efforts have also been devoted to investigate the Dirac electron analogue of optical phenomena, such as negative refraction, Goos-Hänchen effect, beam collimation and Fabry-Pérot resonances/interferences, in graphene systems^{27,28,29,30,31,32,33,34} and TI materials^10,35,36,37. For instance, Fabry-Pérot type conductance oscillation patterns of Dirac fermions in monolayer graphene p-n junctions^30,34 and giant conductance oscillations in ballistic trilayer graphene Fabry-Pérot interferometers³² have been successfully observed in recent quantum transport experiments. More recently, in contrast to ordinary surface states in common metals, recent STM experiment performed on TI material Sb(111) surface suggests that the Dirac fermions transmit the step barriers with a high probability and the Fabry-Pérot resonance of the topological surface states has been observed¹⁰. Although it is highly challenging in experiments to confine the massless Dirac fermions in the nanoscale quantum corrals³⁸ constructed by adatoms or Fabry-Pérot resonators formed by straight parallel step defects on TI surface, the latest success has been achieved on Bi₂Te₃(111)-based samples³⁹.

Because of its importance both from basic point of interest and to TI-based quantum device applications, in the present paper we address this issue by presenting an attempt at the theoretical evaluation of the Fabry-Pérot resonance problem of the massless Dirac electrons on the TI surface in the presence of double symmetric steps. We show that because of the strong warping effect in the topological surface states, the electronic LDOS confined in the step-well running along y (Γ–M) direction and those in the step-well running along x (Γ-K) direction exhibit anisotropic Fabry-Pérot resonance images. The resonant transmission properties as well as the spin orientation of Dirac fermion in both cases are also influenced remarkably by the warping effect. These findings could be confirmed by STM measurements.

Results

We start from the effective Dirac Hamiltonian for the TI surface which is expressed as^11,19,40

where v_f (~240 meV·nm) is the Fermi velocity, λ (~250 meV·nm³ for Bi₂Te₃) is the warping parameter^9,11,19, σ = {σ_x, σ_y, σ_z} are Pauli matrices acting on spin space and k_± = k_x ± ik_y. For simplicity, here we ignore the spin-independent k²/2m term in the effective Hamiltonian since it just results in particle-hole asymmetry but affects the shape of Fermi surface little. Therefore, the anisotropic Fabry-Pérot resonant states discussed following will not be affected when the particle-hole asymmetry is absent. 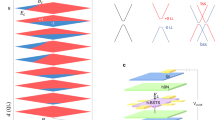The eigenfunction of H₀ is given by ψ_s (k, r) = (ϕ_1,s, siϕ_2,se^iθ)^Te^ik·r, where and s = ±1 corresponds to the upper and lower band dispersion , which is schematically shown in Fig. 1(c). Here, , , where with .

Figure 1

Two symmetric steps on a TI surface with strong warping effect.

(a) Schematics of the symmetric steps and (b) double δ-type barriers. (c) Constant energy contour of ε_s (k) for Bi₂Te₃ TI material with the fermi velocity v_f = 240 meV·nm and the warping parameter λ = 250 meV·nm³.

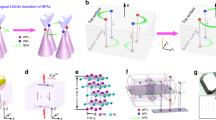
Usually, the straight and parallel steps could be naturally formed in the progress of molecular-beam epitaxy growth, which will result in scattering of quasiparticles on the surface of the sample. Hereafter we consider the problem of massless Dirac electrons confined in a pair of symmetric steps apart 2a along the x or y direction on the surface of a three-dimensional TI, which is schematically shown in Fig. 1(a). The step-edge potential is also illustrated in Fig. 1(b), which is assumed as one-dimensional δ–type.

Steps along the y direction

In what follows, let us consider the double nanoscale parallel steps along the y direction on TI surface with the scattering potential described as δ–type potential barriers^{15,16,20,21,22}

where h is the hight of step and the step edges are located at x₀ = ±a. At this stage, we would like to point out that it is easy, on one side, to treat the boundary conditions for a pair of δ–type potential barriers, while for other types of barriers (such as rectangular, semielliptic and Gaussian profile barriers) the eigenequations of the boundary condition become too tedious and complicated to obtain the analytical results. On the other side, the key physical properties in the step scattering will not be lost by using δ–type barriers herein. Therefore, in this work we choose to employ barrier model (2) for simplicity and clarification.

In the scattering process, we suppose an incident electron plane wave from one side [region I in Fig. 1(a)] with momentum k and energy ε_s will be reflected back to the same side or transmits into the step-well (region II) and then the transmitted part will be reflected between the both steps or transmits further into the other side (region III). Thus, the wave functions could be written as

Here, we have assumed that k_y is a good quantum number and the energy is conserved in the electron scattering process, naively, the reflected and transmitted waves will be characterized by k_f ≡ (−k_x, k_y) = (k, θ_f) and k ≡ (k_x, k_y) = (k, θ) with θ_f = π − θ. Such an assumption is an analogy between electron transport and light propagation since it could be understood in terms of phenomena like reflection and transmission³¹. This results in that ϕ_1,s(−k_x, k_y) = ϕ_1,−s(k_x, k_y) and ϕ_2,s(−k_x, k_y) = ϕ_2,−s(k_x, k_y). and denote the reflection amplitude and tunneling amplitude, respectively. By considering the boundary conditions of wave functions at the step edges x₀ = ±a, we can obtain the amplitudes , , and , seeing the details of the derivation in the section of METHODS.

It is also easy by using Eq. (3) to get the analytical expressions of spin orientation 〈σ〉 = 〈ψ (r)|σ|ψ (r)〉 of Dirac fermion on TI surface in the presence of Fabry-Pérot resonator, which are shown in the part of METHODS. Because of the scattering and interference induced by the double steps, the spin texture of the bands becomes spatially dependent and is modified via the amplitudes , , and , which could be clearly found from Eqs. (12–14). As an example, in Fig. 2(a) we exhibit the spatial distribution of spin orientation for a scattered Dirac fermion with incident angle θ = π/3. It is obvious from Fig. 2(a) that 〈σ_x,y,z〉_x<−a and 〈σ_x,y,z〉_|x|<a in incoming and step-well regions [i.e., region I and II shown in Fig. 2(a)] periodically oscillate with space coordinate x while 〈σ_x,y,z〉_x>a in out-coming region [region III in Fig. 2(c)] are independent on x, which are consistent with the analytical results in Eqs. (12–14). Furthermore, one can also observe from Fig. 2(a) that the spin orientations of 〈σ_x,y,z〉 are discontinuous at the steps x₀ = ±a indicating sudden change of the direction of spin, which is similar to the case of a single step (not shown here for briefness). The numerical results of spin orientation corresponding to Eqs. (12–14) as a function of the direction of in-plane wave-vector are shown in Figs. 2(c–e) and for comparison, the spin orientation for the free Dirac fermion on a clean surface of TI is also shown in Fig. 2(b). In Figs. 2(b–e), the black arrows denote the xy–plane component 〈σ_||〉 = 〈σ_x〉 + i〈σ_y〉, the color background denotes the z component 〈σ_z〉 and the wine curves denote the contours of constant energy. We can see from Fig. 2(b) that for the free Dirac fermion, the xy–plane component 〈σ_||〉 rotates clockwise (s = +1) and the threefold symmetry of 〈σ_z〉 becomes obvious with increasing the Fermi energy due to the warping effect. Comparing with the case of a free Dirac fermion [Fig. 2(b)], due to the quantum interference, the spin orientation of the scattered Dirac fermion located in regions I and II is affected so strongly that on one hand, not only the amplitude of 〈σ_||〉 is changed remarkably but also the clockwise rotation of 〈σ_||〉 is blured, on the other hand, the threefold symmetry of 〈σ_z〉 is broken, see Figs. 2(c) and 2(d). Whereas, for the Dirac fermion transmitted into region III, there are two key points that need to be noticed: i) Both the clockwise rotation of 〈σ_||〉 and the threefold symmetry of 〈σ_z〉 are exact; ii) The amplitude of 〈σ_x,y,z〉_x>a is proportional to the transmittance [Eq. (14)] and thus 〈σ_z〉 exhibits sharp peaks in Fig. 2(e) which is corresponding to resonant tunneling (see the following discussion). Moreover, in the absence of warping effect of surface bands (i.e., d₃ = 0 and k′ = d), the spin orientation 〈σ〉 could be further simplified (see the formulae below Eq. (15) in the METHODS section). Especially, we find in this case that i) 〈σ_y〉 will not oscillate in real-space since it becomes independent on x and ii) the spin of the Dirac fermion in region III is still locked in the surface plane since 〈σ_z〉_x>a = 0.

Figure 2

Spin orientations of Dirac fermions on the surface of TI.

(a) The spatial distribution of spin orientation for Dirac fermions scattered from the double steps, where the incident angle θ = π/3. (b) Spin orientation of free Dirac fermions. (c–e) Spin orientation of scattered Dirac fermions at Region I x = −1.5a (c), region II x = 0.5a (d) and region III (e) on a TI surface with double steps located at ±a. In (b–e) the arrows (color backgrounds) denote the xy–plane component 〈σ_||〉 (z component 〈σ_z〉) and the wine curves denote the constant energy contours. Parameters are chosen as a = 20 nm, s = +1, v_f = 240 meV·nm, warping effect λ = 250 meV·nm³ and .

Now let us turn to discuss the transmission property of Dirac fermions in the Fabry-Pérot resonator on TI surface, which is also irradiative for the explanation of the spin orientation discussed above. Differing from the single step case^15,16,17, there will appear resonant tunneling in two-step or multi-step scattering. We could analytically determine from Eq. (15), that the resonance transmission satisfies the condition of with n an integer number. In other words, for the incoming state with wave vector k = (k, θ), the resonance transmission occurs when the incident angle satisfies the relationship that and the corresponding resonance level is expressed as in the absence of warping effect in the topological surface state. It is easy to check that the reflection coefficient and tunneling amplitudes satisfy the relation of . Furthermore, we should point out that if the plane wave incident from the right side of steps, i.e., from region III, one could also obtain the similar expressions of and and is satisfied, which is the same as that of a single step case. Similar to the case of the optical Fabry-Pérot resonator, and are also determined by the distance between the two mirrors and the incident angle of light and if the absorption is neglected is required because of the conservation of energy. However, differing from the optical case, and of Dirac fermions in the present system are strongly dependent on the nature of bands (warping effect) and the height of barriers seeing the following discussions and formulae in the METHODS section.

The typical results of reflectance and transmission strengths as functions of incident angle θ (the angle of incident wave vector k to the normal direction of steps) are shown in Fig. 3. One can find the resonant tunneling T = 1 (correspondingly, the backscattering is forbidden) at normal incidence (θ = 0) and other special values of θ that satisfy the resonance conditions, see the red curves in Fig. 3. Another interesting phenomenon should be noticed that although the spin orientation of Dirac fermion rotates in the step-well region due to the quantum interference, when the resonant tunneling occurs, its orientation in the out-coming region will turn back to that in the incoming region, i.e., when T = 1 and R = 0, see Eqs. (12) and (14). In other words, the spin of transmitted Dirac fermion points along the same direction as that for the incident Dirac fermion when it resonantly tunnels through single- or multiple-step. It can also be found from Fig. 3 that with increasing the energy of incident electron, the resonant tunneling becomes more remarkable. By a comparison of Fig. 3(b) and Fig. 3(c), one can see that the curves of reflectance and transmittance strengths are reformed due to the influence of strong warping effect, but the incident angles corresponding to the resonant tunneling are unaltered.

Figure 3

Transmittance (red) and reflectance (blue) strengths of Dirac fermions on the surface of TI with two symmetric steps grown along the y direction.

(a–b) Transmittance T and reflectance R vs. the incident angle θ without warping effect. (c) T and R with warping effect. The momentum is chosen as k = 0.2 nm⁻¹ in (a) and k = 1.3 nm⁻¹ in (b) and (c). Other parameters are the same as those in Fig. 2.

In order to determine the discrete resonance energy levels confined in the step-well, we plot the transmittance strength versus the wave vector components k_x and k_y without [Fig. 4(a)] and with [Fig. 4(c)] warping effect. Correspondingly, the colored background in Figs. 4(b) and 4(d) are the transmittance strength versus the energy ε of electron and the wave vector component k_y. With increasing energy, it is clear that the warping effect becomes strong and obvious. We can observe the resonant tunneling peaks corresponding to the quantized k_x and from these numerical results of T the resonance condition can be also concluded as , which is consistent with the analytical results obtained from the expression for in the absence of warping term [see Eq. (15)]. Substituting this back into the band dispersion ε_s (k), one can obtain the discrete resonance energy levels confined in the step-well, which are also shown in Figs. 4(b) and 4(d) by the black dotted curves. It is clear that the resonance are perfectly consistent with the resonant tunneling peaks.

Figure 4

Resonance transmission of Dirac fermions on the surface of TI with two symmetric steps grown along the y direction.

(a–b) Transmittance contour plot versus k_x and k_y and versus k_y and ε for the case without warping effect. (c–d) Transmittance for the case with warping effect. The black dotted curves in (b) and (d) are for the resonance energy ε_n,s. The parameters are the same as those in Fig. 2.

After obtaining the resonance energy levels, one can easily get the LDOS between the double steps, which is expressed as

In order to observe the Fabry-Pérot resonant states more clearly, we subtract the contributions of the averaged background and only consider the change in the LDOS Δρ_II (r, ε) due to the step scattering in following calculations.

Figure 5 shows the energy and position dependence of the LDOS confined in a symmetric step-well along the y (Γ–M) direction on TI surface. One can clearly see the obvious quantum confinement and the LDOS images are symmetric because our Fabry-Pérot step-well model is symmetric in the calculations herein. The number of resonant peaks increases with increasing energy, which is consistent with the resonance properties of transmittance shown above. In our calculations, the ground state confined in the Fabry-Pérot resonator is located at 40 meV, while the first excited state with one node lies at 55 meV. When comparing Fig. 5(a) with Fig. 5(b), it is surprising to find that there exists a strong enhancement in the LDOS in the energy region from 120 meV to 200 meV when the warping effect is taken into account in the calculations (λ ≠ 0), while at other energy regions the resonance modes are similar to the case in the absence of warping effect (λ = 0). The differences in peak intensity and resonance period could be more clearly observed from the curves in Figs. 5(c)–(e). In addition, we have also checked other step-wells with different widths, the enhancement of the LDOS around the energy region of 120 ~ 200 meV is still remarkable (not shown here). This enhancement is closely related to the occurrence of the flat-band crossover when the k_y-linear positive term, which is the dominate term at low energy, is superposed onto the k_y-square negative term which is dominate at high energy [see Fig. 3(d)]. This bunches the electronic states and therefore results in the enhancement of the LDOS in the observed energy region. One could also qualitatively understand the enhancement of LDOS in the energy region of 120 ~ 200 meV from the view point of the approximation of stationary phase points (SPPs)¹¹. The LDOS is dominated by the SPPs [(k_x, k_y) and (−k_x, k_y)] along the direction of Γ–K on the constant energy contour since most of the contributions to the integral in Eq. (4) are from the vicinity of these points. Therefore, the integral can be broken up into regions between stationary phase points that , where means that the integration of k_y is around SPPs. Taking into account the warping effect, the separation between the resonance levels at energy region of 120 ~ 200 meV (n = 5, 6, 7, 8) is compressed, see the black dotted curves in Fig. 4(d). Thus, the LDOS will be enhanced. While with further increasing of energy, the separation between resonance levels becomes larger and larger, which results in the decrease of LDOS [see Fig. 5(b) and the black curves in Figs. 5(c) and 5(d)]. Additional q-vectors (q = k_f − k_i) apart from the SPPs will blur the LDOS because of the rapidly varying phase factor in the integral of Eq. (4), which has little contribution to the total LDOS.

Figure 5

The change in the LDOS of Dirac electrons confined in the double symmetric steps apart along the y direction on TI surface.

(a) The change in the LDOS Δρ_II (x, ε) confined in the double symmetric δ–type steps apart 2a = 40 nm on TI surface without warping effect. (b) Δρ_II (x, ω) confined in the steps on TI surface with warping effect. (c) Bias dependent LDOS spectra at the center of step-well x = 0. (d–e) Spatially dependent LDOS spectra within finite bias ε = 150 meV and ε = 350 meV, respectively. The blue (black) curves are for the case of without (with) warping effect. All the other parameters are the same as those in Fig. 2.

The numerical results of LDOS outside the step-well Δρ_I (r, ε) are plotted in Fig. 6. We can see from Fig. 6(a) that resonant tunneling of the Dirac fermions is obvious in the contour plot of energy-resolved modulations of the LDOS, which is consistent with the above discussions of the transmittance. Different from the single step case, the quantum interferences due to the multi-step scattering is clear in the present Fabry-Pérot resonator and the warping effect is also remarkable [comparing the black curves with the blue curves in Figs. 6(b) and 6(c)] with the increase of energy. In addition, the character of the Friedel-type decaying oscillations in the present case is similar to the single step case. Our theoretical simulations are qualitatively consistent with the STM experimental observations of the Fabry–Pérot resonance of the topological surface states on the Sb(111) surface¹⁰ and the theoretical methods used in this work should be useful for the explanations of the related STM experiments. One should also notice that because k_y keeps unchanged in the scattering process, the LDOS oscillates only in the perpendicular direction of steps, which is the same as the spin orientation.

Figure 6

The change in the LDOS outside of the double steps along the y direction on TI surface with warping effect.

(a) The change in the LDOS Δρ_I (x, ε) versus x and ε. (b) and (c) spatially dependent Δρ_I (x, ε) spectra within finite bias ε = 150 meV and ε = 350 meV, respectively. The blue (black) curves are for the case of without (with) warping effect.

Steps along the x direction

Now we switch gears and consider the case of steps along the x (Γ–K) direction. Due to the hexagonal warping term in the Hamiltonian (1), the x (Γ–K) and y (Γ–M) directions are inequivalent, which could be seen from the constant energy contour shown in Fig. 1(c). Moreover, the warping term in Hamiltonian (1) is represented as in the real space, therefore, it is naturally expected that different orientation of steps leads to different Fabry-Pérot resonant features in the LDOS and in the reflection/transmittance properties. For the steps along the x (Γ–K) direction, the wave function in each region should be written as

In this case, the reflected wave vectors will be characterized by k_f ≡ (k_x, −k_y) = (k, −θ), which results in ϕ_1,s(k_x, −k_y) = ϕ_1,s(k_x, k_y) and ϕ_2,s(k_x, −k_y) = ϕ_2,s(k_x, k_y). Following the same method used above to consider the boundary conditions at y₀ = ±a, one could also easily get the coefficients , , and [see Eq. (16) shown in the section of METHODS].

The reflectance and transmittance strengths for this case are shown in Fig. 7. Similar to the case of steps along y (Γ–M) direction, we can observe the resonant tunneling herein and the resonance condition could be concluded as . However, the transmittance mirages and the quantized resonance energy are different from those for the steps along y (Γ–M) direction, which could be clearly observed by comparing Fig. 7 with Fig. 4. Here, the quantized energy dispersion is a result of the superposition between the k_x-linear positive term and the k_x-cubic positive term. Therefore, the aforementioned flatband crossover cannot occur in the present case, as verified in Fig. 7. Notice that θ in Fig. 7 is defined in the same way as in Fig. 4, i.e., the angle of incident wave vector to the positive x axis. Besides, one could derive the spin orientation in the present case and the anisotropy could also be found in the spin orientation since it is related to the coefficients , , and (not shown for briefness).

Figure 7

Transmittance and reflectance strengths of Dirac fermions on the surface of TI with two symmetric steps grown along the x direction.

(a) Transmittance T and reflectance R versus the incident angle θ. (b) Transmittance contourplot vs k_x and k_y and (c) transmittance contourplot vs k_x and ε (c). The warping effect is taken into account in calculations. k = 1.3 nm⁻¹ in (a). The black dotted curves in (c) are for the resonance energy ε_n,k.

The LDOS results for this case are illustrated in Fig. 8. When the warping effect is taken into account, the Fabry-Pérot-like resonance of LDOS confined in the step-well along the x (Γ–K) direction is quite different from the case of steps along the y (Γ–M) direction, which indicates the anisotropic step-scattering character on the TI surface. In this case, the LDOS is dominated by the SPPs along Γ–M direction on the constant energy contour. Especially, the Fabry-Pérot resonance is enhanced [see Fig. 8(b)] around 300 ~ 350 meV in this case since separation between the resonance levels at this energy region is compressed [see the black dotted curves in Fig. 7(c)] due to the warping effect. These interesting anisotropic Fabry-Pérot resonance states confined within nano-steps on the TI surface can not be observed on conventional metal surface or graphene.

Figure 8

Δρ_II(y, ω) of Dirac electrons confined in the double symmetric δ–type steps apart 2a = 40 nm along the x direction on TI surface.

The arrangement is the same as in Fig. 5.

Discussion

Previous STM experiment⁹ and theory¹¹ about the scattering of surface states off single step edges in TI materials Bi₂Se₃ and Bi₂Te₃ in which the warping effect is strong suggested that the power law decay of the standing waves could be modulated with increasing the Fermi level due to the strong warping effect. Based on the above results, we would like to clarify that the experimental relevance of the anisotropic Fabry-Pérot-like resonances states on TI surface will also strongly depend on whether the Fermi level lies close the Dirac point or lies far from the Dirac point so that transport at Fermi level can get strongly effect by warping. The modulation of Fermi level could be easily realized at present experimental conditions by appropriate doping. Chen et al.⁴¹ experimentally suggested that the Fermi level of Bi₂Te₃ can be tuned to intersect only the surface states with strong warping effect and a full energy gap for the bulk states was clearly observed in the angle-resolved photoemission spectroscopy experiment. This indicates that as the Fermi level goes away from the Dirac point, although the angle between spin and momentum is no longer locked in the surface plane since an additional component of out of plane orientation of spin is raised by the warping effect, the bulk disorder may play a weak role in the scattering process of topological surface states. Thereby, we have not considered the role of the bulk disorder in our calculations.

Furthermore, on one side, similar to the case of scattering of surface states caused by single-step defect on the surface of TI^15,16,17, anisotropic transmittance and decay of LDOS outside of the nano-step well has also been observed in our studies due to the strong warping effect; On the other side, however, apart from various details of the model, the major distinctive features of our study are (i) the resonance and interference behaviors of Dirac fermions transmitting double step barriers as well as the corresponding resonance energy levels [Figs. 3, 4, 7] and (ii) the anisotropic Fabry-Pérot resonant states confined within nano-step wells grown along different high symmetry directions on TI surface in the presence of strong warping effect in surface states. Recently, an STM measurement showed that the Fabry-Pérot resonance of the topological surface states on Sb(111) surface with multiple asymmetric steps has been successfully observed¹⁰. The high-quality Fabry-Pérot interferences of Dirac fermions in graphene-based devices have also been achieved in recent quantum transport experiments^30,32,34. More recently, both the quantum confinement of massless Dirac fermions in nanoscale quantum corrals surrounded by Bi-bilayer on Bi₂Te₃ surface³⁹ and the anisotropic scattering of surface state electrons at a point defect on Bi(111) surface⁴² have been experimentally detected. These experimental observations indicate that our methods should be helpful for understanding these experimental findings and we expect that the anisotropic Fabry-Pérot resonance states found in this work could be confirmed in future STM experiments.

In summary, the Fabry-Pérot-like resonances of massless Dirac electron confined within symmetric steps along the x (Γ–K) or y (Γ–M) directions on TI surface have been studied. The analytical expressions for the spin orientations, reflectance and transmission were obtained in the presence of the warping effect. We found that the spin orientation of the Dirac fermion rotates in the step-well region due to the quantum interference, but the transmitted Dirac fermion points along the same direction of the incident fermionic spin when it resonantly tunnels through the step-well. Particularly, because of the strong warping effect in the topological surface state, the spin is no longer locked in the surface plane and the electronic LDOS image confined in the step-well running along Γ–K direction is remarkably different from that in the step-well running along Γ–M direction. The resonant transmittance properties as well as the spin orientation of topological surface states in both cases are also different due to the warping effect. The formula obtained here can be extended to symmetric/asymmetric multi-step cases as well as spin polarized cases. Also, our anisotropic results, which can not be observed in the conventional metal surface and graphene system, may provide new insights in constructing a TI-based Dirac electron Fabry-Pérot wavevector filter, which is analogous to the optical Fabry-Pérot filter. While differing from the optical Fabry–Pérot cavity, which could be used to store photons in a gravitational wave detection, the Fabry-Pérot cavity discussed here may be useful for confining and storing Dirac electrons.

Methods

We derive an equation of continuation of wave functions at boundaries to get the coefficients , , and for the case of the steps grown along the y (Γ–M) direction, which is used to calculate the LDOS in our system. Within the Eq. (3), one could get the total wavefunction as

where Θ(z) is the step function. Now we consider the property of wavefunction at x₀ = ±a respectively. Substituting Eq. (6) into the Hamiltonian (1) in real space and plus the δ–type potential, we have

Integrating both sides of the Eq. (7) near the points x₀ = ±a,

we have the following algebraic equations

where the parameters are expressed as

From Eq. (9), one can get the coefficients , , and . In the presence of the warping effect, the coefficients are easily written as

where M = (a₂b₁ − a₁b₂) (c₃f₁ − c₁f₃) − (a₃b₁ − a₁b₃) (c₂f₁ − c₁f₂), γ = (a₀b₃ − a₃b₀) (c₁f₂ − c₂f₁) + (a₂b₀ − a₀b₂) (c₁f₃ − c₃f₁), α = (a₀b₁ − a₁b₀) (c₁f₃ − c₃f₁), β = (a₁b₀ − a₀b₁) (c₁f₂ − c₂f₁) and τ = (a₁b₀ − a₀b₁) (c₂f₃ − c₃f₂). Here, and are dimensionless variables. We should point out that the properties of Dirac δ-function that and have been used in the derivations of Eq. (9). After obtaining the wavefunctions, we could easily get the analytical expressions of spin orientation 〈σ〉 = 〈ψ(r)|σ|ψ(r)〉 of Dirac fermions on TI surface in the presence of Fabry-Pérot resonator. In the region I (incoming region) in Fig. 1(a), we have

Similarly, in the region II (step-well region), we have

and in the region III (out-coming region), we have

In particular, if the warping effect is ignored (λ = 0) in the derivations, the coefficients should be reduced to the following simpler form that

where and r_± = s (1 + u²) cos θ ± 2. Correspondingly, the spin orientation without considering the warping effect could be simplified and we have in region I , and , in region II , and and in region III , and 〈σ_z〉_x>a = 0.

Furthermore, for the case of the steps grown along the x (Γ–K) direction, with the same method above to treat the wave functions (5), we could also get the coefficients , , and , where M, α, β, γ and τ have the same form shown above but with the parameters expressed as

After obtaining these coefficients, one could get the LDOS confined in the nanosteps by employing Eq. (4) in the text.