Introduction

High-Q optical resonances in periodic thin films are connected conceptually to embedded bound states which do not reradiate external waves. These were originally proposed in hypothetical quantum systems by von Neumann and Wigner1. In such systems, a completely bound state exists at an energy level above the lowest continuum level. Marinica et al. proposed a symmetric double-grating structure to support embedded photonic bound states by coupling between two identical resonant grating layers2. Hsu et al. experimentally showed a diverging radiation Q factor as a signature of embedded bound states in a single layer of a freestanding Si3N4 thin-film photonic crystal3. More recently, complete 3-dimensional optical confinement in open scattering systems was suggested using layered plasmonic nanoparticles4,5.

In real optical systems, embedded bound states are excited or probed in an asymptotic manner3,6 since at the exact condition they do not interact with the continuum states that contribute to the observation in the far field. In other words, what we actually measure in the laboratory is the resonance response of leaky modes that asymptotically approach a targeted bound state creating a virtual singularity in the spectrum. In this aspect, an important question concerns the properties of the resonance Q factor (Q) as the configuration approaches the exact bound state condition. A related point is the maximal achievable field enhancement. Obviously, field enhancement or excitation strength does not simply increase with diverging Q because the mode excitation vanishes at the exact point of Q = ∞ as long as no significant non-linear coupling occurs between the bound state and the external continuum7. Therefore, there must exist an optimum quasi-embedded bound-state resonance configuration somewhere in-between highly leaky and completely trapped mode conditions. This is a crucial problem for sensing, nonlinear applications and cavity-QED problems. Nevertheless, this issue has not been discussed in detail to date. Importantly, leaky-mode resonance with intermediate Q and associated strong field enhancement is currently of high interest as they have versatile properties enabling high-performance optical filters8, label-free biosensors9, lossless mirrors10, dielectric metasurfaces11,12, dielectric-based optical magnetism13 and many others14,15.

In this paper, we study resonance Q factors and field enhancement effects originating in embedded photonic bound states in periodic Si thin-film structures. We show that a 700-nm-thick fully etched Si thin-film grating supports a symmetry-protected bound state at zero in-plane wave vector (k|| = 0) with ultrahigh resonance Q and electric field intensity enhancement factors exceeding 108. The same structure also supports a quasi-embedded bound state at k|| ≠ 0 in spite of vertical asymmetry of the structure. Field enhancement factors of these photonic resonances show a non-trivial relation with the resonance Q factors in the presence of absorption. We explain this relation with an analytic theory based on the coupled-mode theory of optical Fano resonances. As a crucial factor for applying this device class to practical applications, we discuss methods to maximize resonance Q factors for a given, unavoidable level of material dissipation.

Spectral and angular properties

We consider a subwavelength periodic thin-film structure consisting of a crystalline Si grating with period Λ, fill factor F and thickness d between an air half space and a silica substrate (nsub = 1.45) as shown in Fig. 1a. Polarization of the incident optical field is defined in reference to the plane of incidence: transverse electric (TE) polarization for the electric field perpendicular to the plane of incidence and transverse magnetic (TM) polarization for the magnetic field perpendicular to the plane of incidence. θ denotes the angle of incidence. We use the rigorous coupled-wave analysis16 for numerical calculation of the spectral response and associated internal field properties. We model the crystalline Si with frequency dispersive complex refractive index nSi(λ) = nR(λ) + ikI(λ) and use nR and kI values listed in17.

Figure 1
figure 1

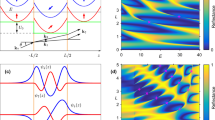
Geometry of the problem and spectral response of an exemplary structure.

(a) Schematic of a high-Q resonance element consisting of a fully etched crystalline Si (c-Si) grating on SiO2 substrate. (b–d) Optical response of a c-Si thin-film grating with Λ = 660 nm, F = 0.7 and d = 700 nm under TM-polarized light incidence. (b) Zero-order transmittance (T0) as a function of wavelength and angle of incidence. (c,d) show magnified T0 maps for regions A and B, respectively.

Full size image

Figure 1b shows the angle-dependent zero-order transmission (T0) spectrum through a c-Si thin-film grating with Λ = 660 nm, F = 0.7 and d = 700 nm under TM-polarized plane-wave incidence. The T0 spectrum shows broad high and low transmission regions accommodating many sharp resonance features. Here, we focus on the sharp resonance features for further analysis. The two features in regions A and B show vanishingly narrow resonance bandwidth as θ approaches 0° and 15.4°, respectively. These regions are magnified in Fig. 1c,d for clearer confirmation of the vanishing bandwidth. These high-Q resonance excitations produce extremely sharp spectral profiles as shown in Fig. 2. The resonance bandwidth approaches 2.9 fm for the region-A resonance and 9.2 pm for the region-B resonance. The corresponding resonance Q-factors are 5.46 × 108 and 1.62 × 105 for resonance in region A and B, respectively.

Figure 2
figure 2

Spectral profiles of zero-order transmittance for several sampled angles of incidence in region A (a) and region B (b).

Full size image

Internal field distributions reveal the nature of the modes inducing these high-Q resonances. The field distributions associated with the region-A resonance are shown in Fig. 3a–c when the field enhancement becomes maximal at λ = 1578.547 nm and θ = 0.00125°. We will explain the reason why the field enhancement maximum occurs at this particular angle of incidence later in this paper. In these field distributions, we note that the electric field intensity |E|2 inside the Si ridges and their surfaces is enhanced by a factor exceeding 108. Hence this resonance excitation is highly desirable for surface-emitting Si-Raman amplifiers/lasers. In addition, it is of great interest to optimize the proposed device class in liquid environment for its application as efficient surface-enhanced Raman templates where at least 107–108 scale electric field enhancement factor is required for single-molecule-level detection sensitivity18. The field distributions show that each Si ridge excites a typical radiation patterns of a cylindrical electric dipole aligned with surface normal axis. The tangential field components (Hy and Ex) are anti-symmetric with respect to the mirror-symmetry plane of the structure, i.e., y-z plane in our case. Therefore, leakage radiation to the surface normal direction is forbidden because of symmetry incompatibility with the external radiation whose tangential field components are symmetric with respect to the mirror-symmetry plane. Leakage radiation to the off-normal direction is also forbidden due to the subwavelength periodicity. This property explains the vanishingly narrow resonance bandwidth of the region-A resonance as θ → 0°. This type of radiation decay suppression is also closely related to destructive interference between emitted radiation fields from two counter-propagating leaky guided modes for standing-wave conditions at either one of two edges of a stopband19,20.

Figure 3
figure 3

Field distributions associated with the high-Q resonance features in (a–c) region A and (d–f) region B. Corresponding wavelengths and angles of incidence are selected when the field enhancement becomes maximal. For (a–c), λ = 1578.457 nm and θ = 0.00125°. For (d–f), λ = 1493.849 nm and θ = 15.4°. Note H and E denote magnetic and electric field amplitudes, respectively and the values are normalized by incident field amplitudes.

Full size image

In contrast, the region B resonance is not explained by the mode’s symmetry incompatibility with the external radiation fields or interference properties for standing-wave conditions because the resonance bandwidth vanishes for non-zero angle θ → 15.4° and the incident fields are not necessarily symmetric or anti-symmetric with respect to the mirror-symmetry plane of the structure. Instead, the physical origin of the ultrahigh-Q resonance in region B is related to simultaneous suppression of the leakage radiation amplitudes to the zero-order waves in air cover and silica substrate. This effect involves interference between partial leakage radiations from different Bloch modes and complex interaction of evanescent fields at the top and bottom interfaces of the film3,21. The internal field distributions associated with the region B resonance are shown in Fig. 3d–f and we confirm the electric field intensity enhancement factor in the order of 105.

Resonance Q factors and field enhancement

Considering applications of high-Q resonances in periodic thin films to biochemical sensors, SERS templates and nonlinear optical components, the resonance Q factor Q and associated field intensity enhancement factor W are important figures. We further investigate dependences of these parameters on the excitation condition and derive a useful relation between Q and W in the presence of material dissipation that is unavoidable due to internal absorption and diffuse scattering by film imperfections such as surface roughness, vacancies and grain boundaries.

Following the conventional terminology, we define the total resonance Q factor Qtot ≡ λ0/Δλ = ω0/2(γA + γR), where λ0 is resonance center wavelength, Δλ is full-width at half-maximum of the resonance, ω0 is angular frequency of the resonance center and γA and γR denote partial damping rates due to the material dissipation and leakage radiation, respectively. We also define partial resonance Q factors QA ≡ ω0/2γA as dissipation Q factor and QR ≡ ω0/2γR as radiation Q factor. The total and partial Q factors are related by 1/Qtot = 1/QA + 1/QR. For quantitative analysis of the field enhancement effect, we define two electric field intensity enhancement factors

for the volume-average intensity inside the Si ridges and

for the surface-average intensity on the surface exposed to the air, where E denotes electric field, E0 is incident electric field amplitude, dV is infinitesimal volume and dS is infinitesimal surface area. The two enhancement factors WV and WS are useful parameters in consideration of a resonance element as a nonlinear optical device using the film’s native optical nonlinearity and a SERS template for molecular detection systems, respectively.

We estimate resonance Q factors QA, QR and Qtot and field enhancement factors WV and WS for our simulated cases as shown in Figs 4 and 5 for the region A and B resonances, respectively. For resonance Q factor estimation, we use the absorbance analysis method established in22,23,24. The field enhancement factors by the definition in Eqs. (1) and (2) are directly obtained from the calculated field distributions due to the rigorous coupled-wave analysis.

Figure 4
figure 4

Field enhancement factors for critically coupled resonances in region A.

(a) Partial and total resonance Q-factors. (b) Electric field intensity enhancement factors.

Full size image
Figure 5
figure 5

Field enhancement factors for over-coupled resonances in region B.

(a) Total resonance Q-factor Qtot. (b) Electric field intensity enhancement factors. Note that QA = 4.2~4.4 × 108 is much higher than QR ≈ Qtot in region B, implying that the region B resonances are highly over-coupled.

Full size image

Figure 4a shows the dependences of QA, QR and Qtot on the angle of incidence θ for the region A resonance. The radiation Q factor QR is increasing with decreasing angle of incidence because of the symmetry incompatibility as discussed previously. In contrast, the dissipation Q factor QA is almost constant because the modal field distribution does not remarkably change the portion of field energy inside the Si ridges with the change in θ. Therefore, the total Q factor Qtot increases with QR for the large angle-of-incidence range of θ > 0.01° and becomes saturated at QA = 5.46 × 108 for the small angle-of-incidence range of θ < 0.001°. Dependences of the field enhancement factors are quite distinguished from those of resonance Q factors as shown in Fig. 4b. Both WV and WS increase with increasing Qtot for the large angle-of-incidence range of θ > 0.01°, they are maximized at θ = 0.00125° where QA = QR and they eventually show high slope decrease in the small angle-of-incidence range of θ < 0.001° although the total resonance Q factor is almost constant in this angle-of-incidence range.

We explain this non-trivial property of field enhancement factors on the basis of interference effects associated with generic optical Fano resonances. Using the coupled-mode theory of optical Fano resonances23,25, the energy stored in the resonance mode at the resonance center is expressed by

where ηR ≡ γR/(γA + γR) = Qtot/QR is the radiation probability of the resonance mode, C ≡ γ1/γR with γ1 denoting the partial radiation decay rate to the reflected wave is the relative strength of radiation coupling of the resonance mode with the reflected wave, P0 is the power delivered by the incident wave and t0 ≡ 2π/ω0 is the optical cycle at the resonance center. According to the Lorentz reciprocity theorem for electromagnetic fields, the coupling strength constant C also can be interpreted as a relative coupling strength of the resonance mode with the incident wave. Field enhancement factors WV and WS are directly proportional to the ratio of the energy U stored in the resonance mode to the portion of the incoming energy CP0t0 coupled with the resonance mode for an optical cycle. Following this argument, we define a general field enhancement factor W0 such that

Equation (4) with the partial resonance Q factors QA and QR found in Fig. 4a quantitatively describes the dependence of WV and WS on the angle of incidence as shown in Fig. 4b.

It is obvious in Eq. (4) that the field enhancement does not simply increase with the total Q factor Qtot but it has the maximum at the critical coupling condition where ηR = 1/2, or QR = QA = 2Qtot equivalently. This is a result of a well-known effect of destructive interference of the resonant and non-resonant pathways in the reflected and transmitted waves. At the critical coupling condition, the destructive interference becomes strongest because the two contributions of the resonant and non-resonant pathways to the outgoing waves have the same intensities with π phase difference. This intensity and phase property is dictated by the time-reversal symmetry of the wave coupling processes22,23,25.

For under-coupled resonances with ηR < 1/2 and QR > QA, intensity of the resonant contribution is not strong enough to cancel the non-resonant contribution and hence the light trapping effect is not as strong as for the critically coupled resonances. Alternatively, the field enhancement for an under-coupled resonance does not reach its obtainable maximum with a given Qtot because the rate of radiative energy coupling from the incident wave to the resonance mode is slower than the internal damping rate due to the material dissipation. For highly under-coupled resonances with ηR ≪ 1/2 and QR ≫ QA, Eq. (4) reduces to W0 ≈ (QA/QR)Qtot/π. Therefore, the field enhancement is suppressed by a factor QA/QR (≪1) from that expected for lossless or highly over-coupled resonances. This explains the high-slope decrease of the field enhancement factors of the region A resonance without substantial decrease in Qtot for the small angle-of-incidence range in Fig. 4b.

In the opposite cases of over-coupled resonances with ηR > 1/2 and QR < QA, the resonant contribution dominates the outgoing wave intensities over that from the non-resonant contribution and hence the trapping effect becomes weaker than that for the critically coupled resonances. Alternatively, an over-coupled resonance can be considered to have an excessive radiation decay that exhausts the localized energy before it reaches its maximum limit for a given amount of material dissipation. Equation (4) for the general field enhancement factor reduces to W0 ≈ Qtot/π for highly over-coupled resonances with ηR ≫1/2 and QR ≪ QA. Therefore, the field enhancement is simply proportional to the total Q factor. This explains the dependences of WV and WS on the angle of incidence for the region B resonance that is highly over coupled with QA ≫ Qtot ≈ QR. Figure 5a,b show the estimated Qtot and field enhancement factors as functions of angle of incidence. We confirm that the volume and surface field enhancement factors (WV and WS) are maximized at the angle of incidence corresponding to the Qtot peak. Note that lossless cases is also considered as a highly over-coupled resonance because lossless resonances satisfy QA = ∞ » QR.

Considering real experiments on ultrahigh-Q resonances and associated strong field enhancement, it is important to optimize the amount of the radiation damping of a resonance in accordance with the material dissipation of thin-film materials. High-index semiconductors, nitrides and metal oxides such as Si, Ge, GaAs, Si3N4, TiO2 and HfO2 are common materials for resonant thin-film devices. The intrinsic dissipation of these materials is unavoidable and highly dependent on the film deposition and lithographic etching conditions that determine grain size, density of vacancies and surface roughness. In addition to the material’s internal absorption, these film imperfections cause diffuse scattering that contributes to extinction coefficients in the order of 10–5 ~ 10–3 26,27,28. Therefore, in order to obtain the strong field enhancement effect, device parameters such as fill factor and modulation depth of the pattern that primarily determine the radiation damping rate of a resonance mode should be properly optimized to satisfy the critical coupling condition for a given level of material dissipation. This factor is even more important in nanostructured plasmonic resonance systems including surface plasmonic biochemical sensors and nonlinear plasmonic metamaterials29,30. In plasmonic metals including Ag, Au, Al and Cu, the ohmic absorption is high in the optical frequency domain and dense surface charges induce strong light scattering even from deep-subwavelength rough features on their surfaces.

Conclusion

In conclusion, we address ultrahigh-Q resonances in a subwavelength Si grating. We show that a strongly modulated c-Si subwavelength grating supports embedded and quasi-embedded photonic bound states with resonance Q and field enhancement factors exceeding 108. We find that in the presence of material dissipation the field enhancement associated with an embedded photonic bound state is not simply proportional to the resonance Q factor because of a particular interference effect generally involved in the resonant light trapping effect. Using the coupled-mode theory of general optical Fano resonances, we derive an analytic expression of the field enhancement factor in terms of the radiation probability and absorption Q factor of a bound state. We confirm quantitative agreement of this expression with rigorous numerical calculation results showing the field enhancement maximized at the critical condition where the radiation Q factor is identical to the absorption Q factor. Therefore, our results provide useful knowledge for designing practical resonance elements in various application areas including SERS-based molecular detection systems, cavity-QED problems and nonlinear optical devices.

Additional Information

How to cite this article: Yoon, J. W. et al. Critical field enhancement of asymptotic optical bound states in the continuum. Sci. Rep. 5, 18301; doi: 10.1038/srep18301 (2015).